80

Conversion from NFA to DFA

In this section, we will discuss the method of converting NFA to its equivalent DFA. In NFA, when a specific input is given to the current state, the machine goes to multiple states. It can have zero, one or more than one move on a given input symbol. On the other hand, in DFA, when a specific input is given to the current state, the machine goes to only one state. DFA has only one move on a given input symbol.

Let, M = (Q, ∑, δ, q0, F) is an NFA which accepts the language L(M). There should be equivalent DFA denoted by M’ = (Q’, ∑’, q0′, δ’, F’) such that L(M) = L(M’).

Steps for converting NFA to DFA:

Step 1: Initially Q’ = ϕ

Step 2: Add q0 of NFA to Q’. Then find the transitions from this start state.

Step 3: In Q’, find the possible set of states for each input symbol. If this set of states is not in Q’, then add it to Q’.

Step 4: In DFA, the final state will be all the states which contain F(final states of NFA)

Example 1:

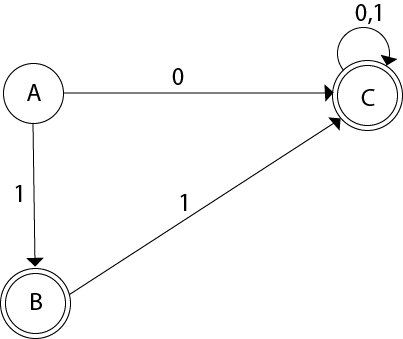
Convert the given NFA to DFA.

Solution: For the given transition diagram we will first construct the transition table.

State	0	1
→q0	q0	q1
q1	{q1, q2}	q1
*q2	q2	{q1, q2}

Now we will obtain δ’ transition for state q0.

The δ’ transition for state q1 is obtained as:

The δ’ transition for state q2 is obtained as:

Now we will obtain δ’ transition on [q1, q2].

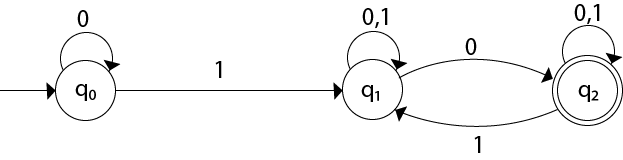
The state [q1, q2] is the final state as well because it contains a final state q2. The transition table for the constructed DFA will be:

State	0	1
→[q0]	[q0]	[q1]
[q1]	[q1, q2]	[q1]
*[q2]	[q2]	[q1, q2]
*[q1, q2]	[q1, q2]	[q1, q2]

The Transition diagram will be:

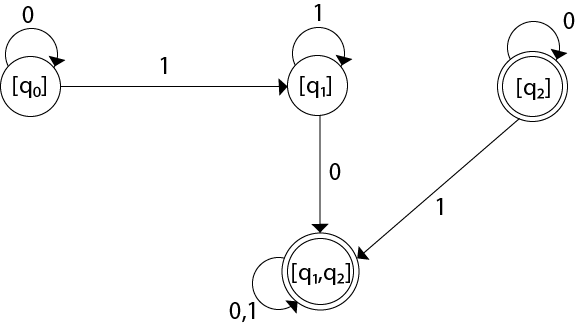
The state q2 can be eliminated because q2 is an unreachable state.

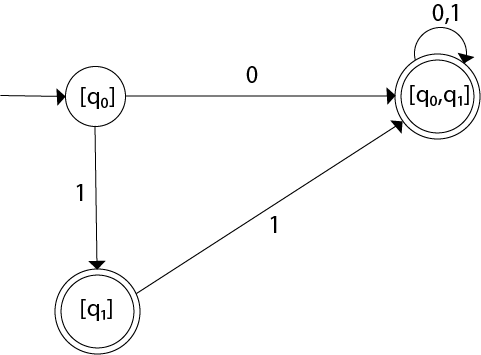
Example 2:

Convert the given NFA to DFA.

Solution: For the given transition diagram we will first construct the transition table.

State	0	1
→q0	{q0, q1}	{q1}
*q1	ϕ	{q0, q1}

Now we will obtain δ’ transition for state q0.

The δ’ transition for state q1 is obtained as:

Now we will obtain δ’ transition on [q0, q1].

Similarly,

As in the given NFA, q1 is a final state, then in DFA wherever, q1 exists that state becomes a final state. Hence in the DFA, final states are [q1] and [q0, q1]. Therefore set of final states F = {[q1], [q0, q1]}.

The transition table for the constructed DFA will be:

State	0	1
→[q0]	[q0, q1]	[q1]
*[q1]	ϕ	[q0, q1]
*[q0, q1]	[q0, q1]	[q0, q1]

The Transition diagram will be:

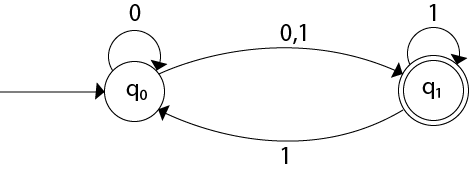
Even we can change the name of the states of DFA.

Suppose

With these new names the DFA will be as follows:

---