Conversion from NFA with ε to DFA
Non-deterministic finite automata(NFA) is a finite automata where for some cases when a specific input is given to the current state, the machine goes to multiple states or more than 1 states. It can contain ε move. It can be represented as M = { Q, ∑, δ, q0, F}.
Where
NFA with ∈ move: If any FA contains ε transaction or move, the finite automata is called NFA with ∈ move.
ε-closure: ε-closure for a given state A means a set of states which can be reached from the state A with only ε(null) move including the state A itself.
Steps for converting NFA with ε to DFA:
Step 1: We will take the ε-closure for the starting state of NFA as a starting state of DFA.
Step 2: Find the states for each input symbol that can be traversed from the present. That means the union of transition value and their closures for each state of NFA present in the current state of DFA.
Step 3: If we found a new state, take it as current state and repeat step 2.
Step 4: Repeat Step 2 and Step 3 until there is no new state present in the transition table of DFA.
Step 5: Mark the states of DFA as a final state which contains the final state of NFA.
Example 1:
Convert the NFA with ε into its equivalent DFA.
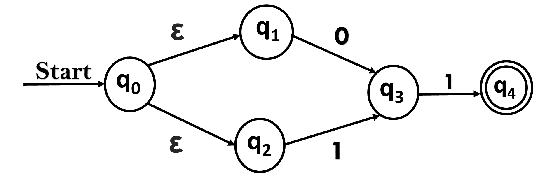
Solution:
Let us obtain ε-closure of each state.
Now, let ε-closure {q0} = {q0, q1, q2} be state A.
Hence
δ'(A, 0) = ε-closure {δ((q0, q1, q2), 0) } = ε-closure {δ(q0, 0) ∪ δ(q1, 0) ∪ δ(q2, 0) } = ε-closure {q3} = {q3} call it as state B. δ'(A, 1) = ε-closure {δ((q0, q1, q2), 1) } = ε-closure {δ((q0, 1) ∪ δ(q1, 1) ∪ δ(q2, 1) } = ε-closure {q3} = {q3} = B. The partial DFA will be
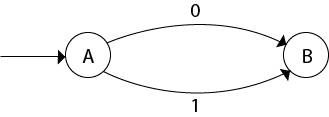
Now,
δ'(B, 0) = ε-closure {δ(q3, 0) } = ϕ δ'(B, 1) = ε-closure {δ(q3, 1) } = ε-closure {q4} = {q4} i.e. state C For state C:
The DFA will be,
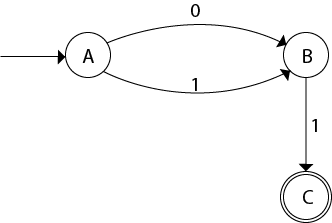
Example 2:
Convert the given NFA into its equivalent DFA.
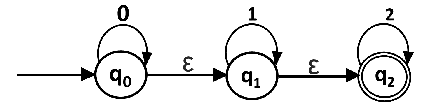
Solution: Let us obtain the ε-closure of each state.
Now we will obtain δ’ transition. Let ε-closure(q0) = {q0, q1, q2} call it as state A.
δ'(A, 0) = ε-closure{δ((q0, q1, q2), 0)} = ε-closure{δ(q0, 0) ∪ δ(q1, 0) ∪ δ(q2, 0)} = ε-closure{q0} = {q0, q1, q2} δ'(A, 1) = ε-closure{δ((q0, q1, q2), 1)} = ε-closure{δ(q0, 1) ∪ δ(q1, 1) ∪ δ(q2, 1)} = ε-closure{q1} = {q1, q2} call it as state B δ'(A, 2) = ε-closure{δ((q0, q1, q2), 2)} = ε-closure{δ(q0, 2) ∪ δ(q1, 2) ∪ δ(q2, 2)} = ε-closure{q2} = {q2} call it state C Thus we have obtained
The partial DFA will be:
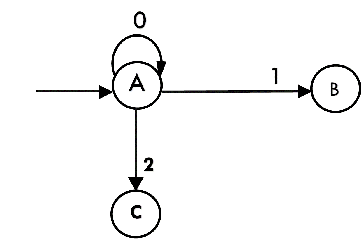
Now we will find the transitions on states B and C for each input.
Hence
δ'(B, 0) = ε-closure{δ((q1, q2), 0)} = ε-closure{δ(q1, 0) ∪ δ(q2, 0)} = ε-closure{ϕ} = ϕ δ'(B, 1) = ε-closure{δ((q1, q2), 1)} = ε-closure{δ(q1, 1) ∪ δ(q2, 1)} = ε-closure{q1} = {q1, q2} i.e. state B itself δ'(B, 2) = ε-closure{δ((q1, q2), 2)} = ε-closure{δ(q1, 2) ∪ δ(q2, 2)} = ε-closure{q2} = {q2} i.e. state C itself Thus we have obtained
The partial transition diagram will be
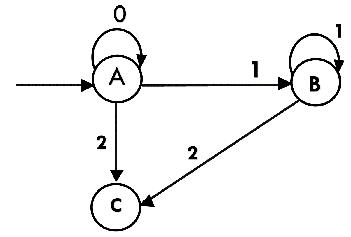
Now we will obtain transitions for C:
δ'(C, 0) = ε-closure{δ(q2, 0)} = ε-closure{ϕ} = ϕ δ'(C, 1) = ε-closure{δ(q2, 1)} = ε-closure{ϕ} = ϕ δ'(C, 2) = ε-closure{δ(q2, 2)} = {q2} Hence the DFA is
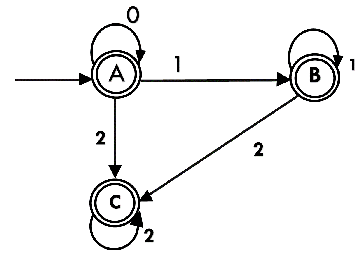
As A = {q0, q1, q2} in which final state q2 lies hence A is final state. B = {q1, q2} in which the state q2 lies hence B is also final state. C = {q2}, the state q2 lies hence C is also a final state.
