Binary Adder-Subtractor
A Binary Adder-Subtractor is a special type of circuit that is used to perform both operations, i.e., Addition and Subtraction. The operation which is going to be used depends on the values contained by the control signal. In Arithmetic Logical Unit, it is one of the most important components.
To work with Binary Adder-Subtractor, it is required that we have knowledge of the XOR gate, Full-Adder, Binary Addition, and subtraction.
For example, we will take two 4-bit binary numbers ‘X’ and ‘Y’ for the operation with digits.
Y0 Y1 Y2 Y3 for Y
The Binary Adder-Subtractor is a combination of 4 Full-Adder, which is able to perform the addition and subtraction of 4-bit binary numbers. The control line determines whether the operation being performed is either subtraction or addition. This determination is done by the binary values 0 and 1, which is hold by K.
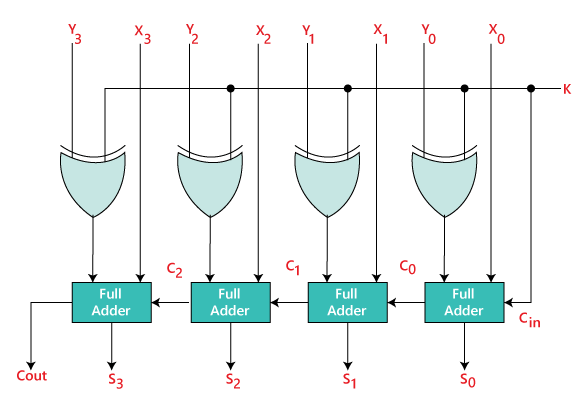
In the above diagram, the control lines of the first Full-Adder is directly coming as its input(input carry C0). The X0 is the least significant bit of A, which is directly inputted in the Full-Adder. The result produced by performing the XOR operation of Y0 and K is the third input of the Binary Adder-Subtractor. The sum/difference(S0) and carry(C0) are the two outputs produced from the First Full-adder.
When the value of K is set to true or 1, the Y0⨁K produce the complement of Y0 as the output. So the operation would be X+Y0‘, which is the 2’s complement subtraction of X and Y. It means when the value of K is 1; the subtraction operation is performed by the binary Adder-Subtractor.
In the same way, when the value of K is set to 0, the Y0⨁K produce Y0 as the output. So the operation would be X+Y0, which is the binary addition of X and Y. It means when the value of K is 0; the addition operation is performed by the binary Adder-Subtractor.
The carry/borrow C0 is treated as the carry/borrow input for the second Full-Adder. The sum/difference S0 defines the least significant bit of the sum/difference of numbers X and Y. Just like X0, the X1, X2, and X3 are faded directly to the 2nd, 3rd, and 4th Full-Adder as an input. The outputs after performing the XOR operation of Y1, Y2, and Y3 inputs with K are the third inputs for 2nd, 3rd, and 4th Full-Adder. The carry C1, C2 are passed as the input to the Full-Adder. Cout is the output carry of the sum/difference. To form the final result, the S1, S2, S3 are recorded with s0. We will use n number of Full-Adder to design the n-bit binary Adder-Subtractor.
Example:
We assume that we have two 3 bit numbers, i.e., X=100 and Y=011, and feed them in Full-Adder as an input.
X0 = 0 X1 = 0 X2 = 1
Y0 = 1 Y1 = 1 & Y2 = 0
For K=0:
Y0⨁K=Y0 and Cin=K=0
So, from first Full-Adder
S0 = X0+Y0+Cin
S0= 0+1+0
S0=1
C0=0
Similarly,
S1 = X1+Y1+C0
S1 = 0+1+0
S1=1 and C1=0
Similarly,
S2 = X2+Y2+C1
S2 = 1+0+0
S2=1 and C2=0
Thus,
X= 100 =4
Y = 011 = 3
Sum = 0111 = 7
For K=1
Y0⨁K=Y0‘ and Cin=k=1
So,
S0 = X0+Y0‘+Cin
S0 = 0+0+1
S0=1 and C0=0
Similarly,
S1 = X1+Y1‘+C0
S1 = 0+0+0
S1=0 and C1=0
Similarly,
S2 = X2+Y2‘+C1
S2 = 1+1+0
S2=0 and C2=0
Thus,
X = 010 = 4
Y = 011 = 3
Difference = 001 = 1
