Binary to BCD code conversion
BCD code plays an important role in digital circuits. The BCD stands for Binary Coded Decimal Number. In BCD code, each digit of the decimal number is represented as its equivalent binary number. So, the LSB and MSB of the decimal numbers are represented as its binary numbers. There are the following steps to convert the binary number to BCD:
- First, we will convert the binary number into decimal.
- We will convert the decimal number into BCD.
Let’s take an example to understand the process of converting a binary number into BCD
Example 1: (11110)2
1. First, convert the given binary number into a decimal number.
Binary Number: (11110)2
Finding Decimal Equivalent of the number:
| Steps | Binary Number | Decimal Number |
|---|---|---|
| 1) | (11110)2 | ((1 × 24) + (1 × 23) + (1 × 22) + (1 × 21) + (0 × 20))10 |
| 2) | (11110)2 | (16 + 8 + 4 + 2 + 0)10 |
| 3) | (11110)2 | (30)10 |
Decimal number of the Binary number (11110)2 is (30)10
2. Now, we convert the decimal to the BCD
We convert each digit of the decimal number into groups of the four-bit binary number.
| Steps | Decimal Number | Conversion |
|---|---|---|
| Step 1 | 3010 | (0011)2 (0000)2 |
| Step 2 | 3010 | (00110000)BCD |
Result:
(11110)2 = (00110000)BCD
Below is the table that contains the BCD code of the decimal and binary number.
| Binary Code | Decimal Number | BCD Code |
|---|---|---|
| A B C D | B4 :B3B2B1B0 | |
| 0 0 0 0 | 0 | 0 : 0 0 0 0 |
| 0 0 0 1 | 1 | 0 : 0 0 0 1 |
| 0 0 1 0 | 2 | 0 : 0 0 1 0 |
| 0 0 1 1 | 3 | 0 : 0 0 1 1 |
| 0 1 0 0 | 4 | 0 : 0 1 0 0 |
| 0 1 0 1 | 5 | 0 : 0 1 0 1 |
| 0 1 1 0 | 6 | 0 : 0 1 1 0 |
| 0 1 1 1 | 7 | 0 : 0 1 1 1 |
| 1 0 0 0 | 8 | 0 : 1 0 0 0 |
| 1 0 0 1 | 9 | 0 : 1 0 0 1 |
| 1 0 1 0 | 10 | 1 : 0 0 0 0 |
| 1 0 1 1 | 11 | 1 : 0 0 0 1 |
| 1 1 0 0 | 12 | 1 : 0 0 1 0 |
| 1 1 0 1 | 13 | 1 : 0 0 1 1 |
| 1 1 1 0 | 14 | 1 : 0 1 0 0 |
| 1 1 1 1 | 15 | 1 : 0 1 0 1 |
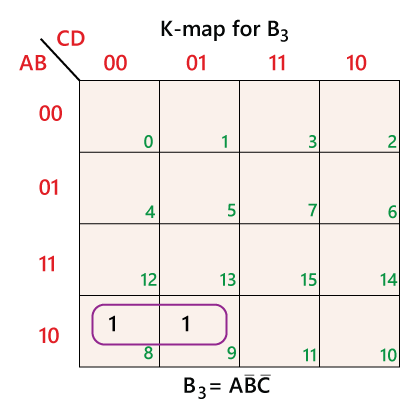
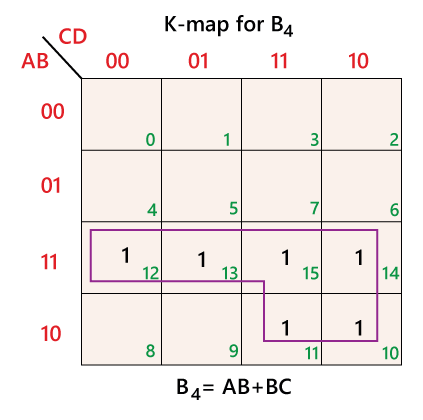
In the above table, the most significant bit of the decimal number is represented by the bit B4, and the least significant bits are represented by B3, B2, B1, and B0. From the above table, we can express the SOP function for different bits of BCD code are as follows:
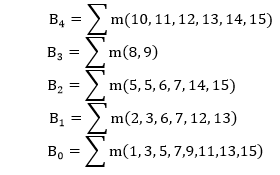
The K-maps of the above SOP functions are as follows:
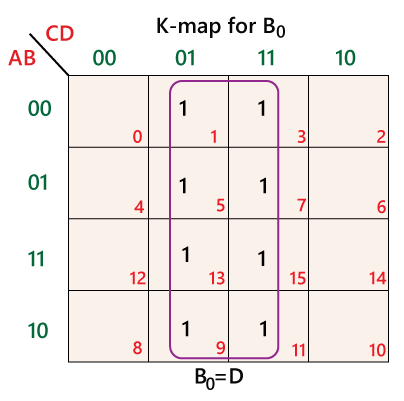
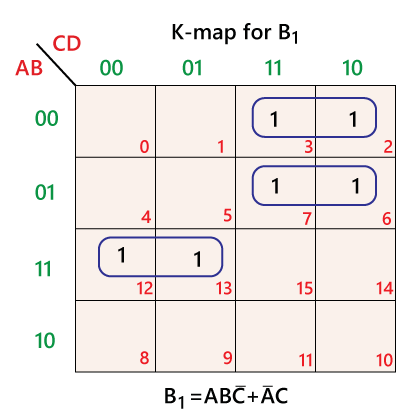
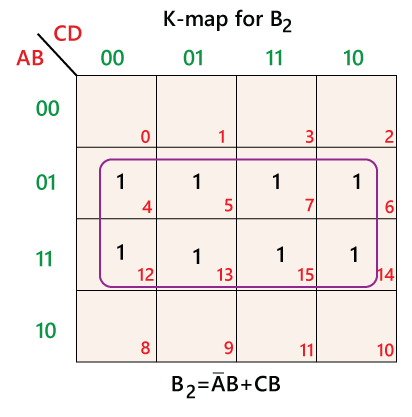
BCD to Binary Conversion
The process of converting BCD code into Binary is opposite to the process of converting Binary code into BCD. There are the following steps to convert the BCD code into Binary:
In the first step, we will convert the BCD number into a decimal by making the four-bit groups and finding the equivalent decimal number for each group.
In the last step, we will convert a decimal number into Binary using the process of converting decimal to binary number.
Example 1: (00101000)BCD
1) Convert BCD to Decimal
Make the groups of 4 digits and find the equivalent decimal number as:
| Steps | BCD Number | Conversion |
|---|---|---|
| Step 1 | (00101000)BCD | (0010)2 (1000)2 |
| Step 2 | (00101000)BCD | (2)10 (8)10 |
| Step 3 | (00101000)BCD | (28)10 |
The decimal number of the given BCD code is: (28)10
2. Convert Decimal to Binary
Use the long division method to convert the decimal number into a binary number as:
| Steps | Operation | Result | Remainder |
|---|---|---|---|
| 1. | 28 / 2 | 14 | 0 |
| 2. | 14 / 2 | 7 | 0 |
| 3. | 7 / 2 | 3 | 1 |
| 4. | 3 / 2 | 1 | 1 |
| 5. | 1 / 2 | 0 | 1 |
Arrange the remainders in the reverse order. So, the LSB of the binary number is the first remainder, and the MSB of the binary number is the last remainder.
The binary number of the decimal number (18)10 is: (11100)2
Result:
(00101000)BCD = (11100)2
