Binary to Gray code conversion
The Binary to Gray code converter is a logical circuit that is used to convert the binary code into its equivalent Gray code. By putting the MSB of 1 below the axis and the MSB of 1 above the axis and reflecting the (n-1) bit code about an axis after 2n-1 rows, we can obtain the n-bit gray code.
The 4-bit binary to gray code conversion table is as follows:
| Decimal Number | 4-bit Binary Code | 4-bit Gray Code |
|---|---|---|
| ABCD | G1G2G3G4 | |
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
In 4-bit gray code, the 3-bit code is reflected against the axis drawn after the 24-1-1th =8th row.
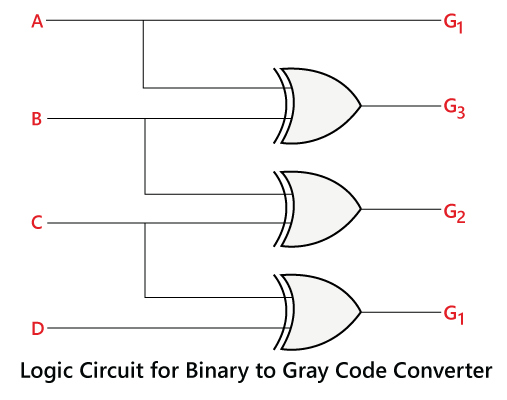
How to Convert Binary to Gray Code
- In the Gray code, the MSB will always be the same as the 1’st bit of the given binary number.
- In order to perform the 2nd bit of the gray code, we perform the exclusive-or (XOR) of the 1’st and 2nd bit of the binary number. It means that if both the bits are different, the result will be one else the result will be 0.
- In order to get the 3rd bit of the gray code, we need to perform the exclusive-or (XOR) of the 2nd and 3rd bit of the binary number. The process remains the same for the 4th bit of the Gray code. Let’s take an example to understand these steps.
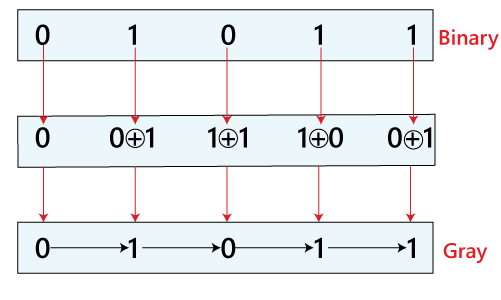
Example
Suppose we have a binary number 01101, which we want to convert into Gray code. There are the following steps which need to perform this conversion:
- As we know that the 1st bit of the Gray code is the same as the MSB of the binary number. In our example, the MSB is 0, so the MSB or 1st bit of the gray code is 0.
- Next, we perform the XOR operation of the 1’st and the second binary number. The 1st bit is 0, and the 2nd bit is 1. Both the bits are different, so the 2nd bit of the Gray code is 1.
- Now, we perform the XOR of the 2nd bit and 3rd bit of the binary number. The 2nd bit is 1, and the 3rd bit is also 1. These bits are the same, so the 3rd bit of the Gray code is 0.
- Again perform the XOR operation of the 3rd and 4th bit of binary number. The 3rd bit is 1, and the 4th bit is 0. As these are different, the 4th bit of the Gray code is 1.
- Lastly, perform the XOR of the 4th bit and 5th bit of the binary number. The 4th bit is 0, and the 5th bit is 1. Both the bits are different, so that the 5th bit of the Gray code is 1.
- The gray code of the binary number 01101 is 01011.
Gray to Binary Code Conversion
The Gray to Binary code converter is a logical circuit that is used to convert the gray code into its equivalent binary code. There is the following circuit used to convert the Gray code to binary number.
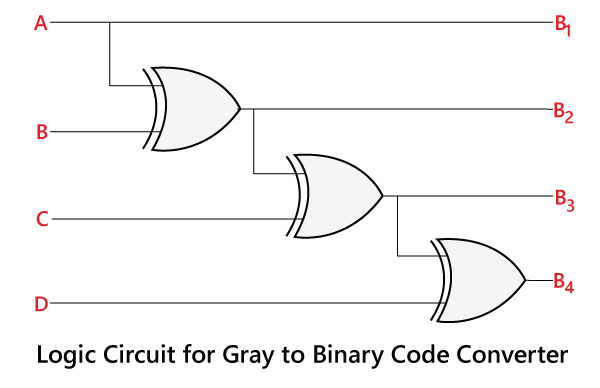
Just like Binary to Gray code conversion; it is also a very simple process. There are the following steps used to convert the Gray code into binary.
- Just like binary to gray, in gray to binary, the 1st bit of the binary number is similar to the MSB of the Gray code.
- The 2nd bit of the binary number is the same as the 1st bit of the binary number when the 2nd bit of the Gray code is 0; otherwise, the 2nd bit is altered bit of the 1st bit of binary number. It means if the 1st bit of the binary is 1, then the 2nd bit is 0, and if it is 0, then the 2nd bit be 1.
- The 2nd step continues for all the bits of the binary number.
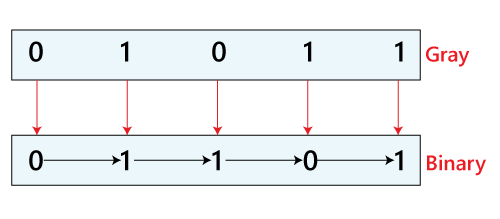
Gray Code to Binary Conversion Example
Suppose we have the Gray code 01011, which we want to convert into a binary number. There are the following steps which we need to perform for the conversion:
- The 1’st bit of the binary number is the same as the MSB of the Gray code. The MSB of the Gray code is 0, so the MSB of the binary number is 0.
- Now, for the 2nd bit, we check the 2nd bit of the Gray code. The 2nd bit of the Gray code is 1, so the 2nd bit of the binary number is one that is altered number of 1st
- The next bit of the Gray code is 0; the 3rd bit is the same as the 2nd bit of the Gray code, i.e., 1.
- The 4th bit of the Gray code is 1; the 4th bit of the binary number is 0 that is the altered number of the 3rd
- The 5th bit of the Gray code is 1; the 5th bit of the binary number is 1; that is the altered number of the 4th bit of the binary number.
- So, the binary number of the Gray code 01011 is 01101.
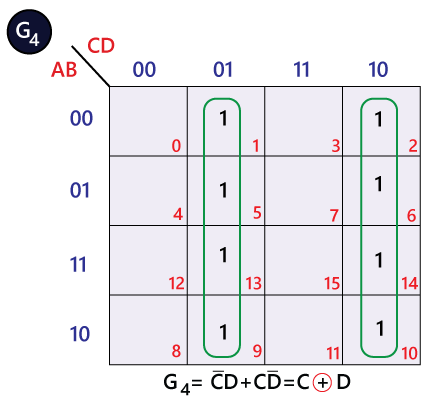
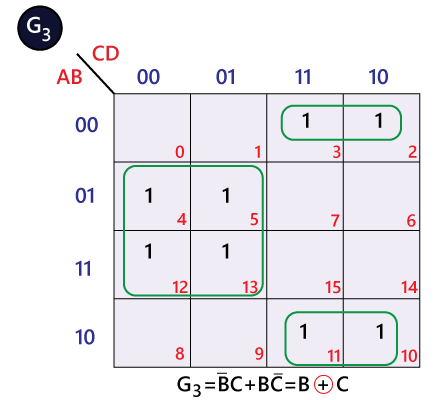
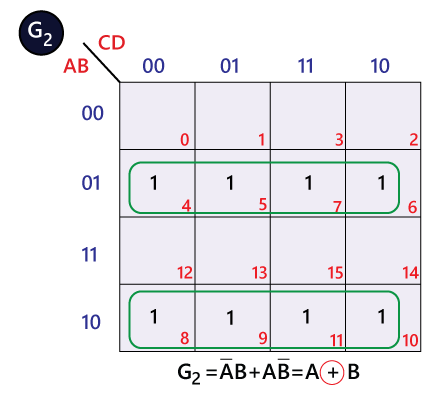
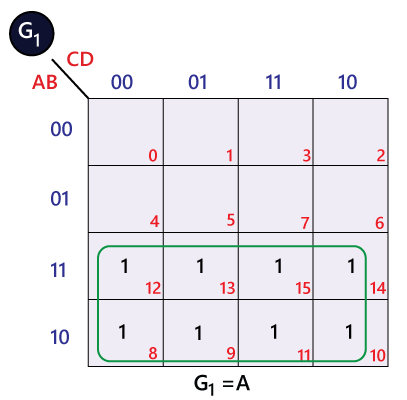
The bits of 4-bit Gray code are considered as G4G3G2G1. Now from the conversion table,
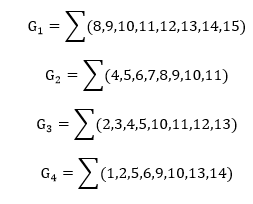
The Karnaugh maps (K-maps) for G4, G3, G2, and G1 are as follows: