225

Binomial Heap

In this article, we will discuss the binomial heap. Before start discussing the topic, we should first understand some basic terms such as heap, min-heap, max-heap, and binomial tree.

What is a heap?

A heap is a complete binary tree, and the binary tree is a tree in which the node can have utmost two children. There are two types of heap that are defined as follows –

• Min Heap: The value of the parent node should be less than or equal to either of its children.
  Mathematically, the min-heap can be defined as –
  A[Parent(i)] <= A[i]
• Max Heap: The value of the parent node is greater than or equal to its children.
  Mathematically, the max-heap can be defined as –
  A[Parent(i)] >= A[i]

What is a Binomial tree?

A Binomial tree B_k is an ordered tree defined recursively, where k is defined as the order of the binomial tree.

• If the binomial tree is represented as B₀, then the tree consists of a single node.
• In general terms, B_k consists of two binomial trees, i.e., B_k-1 and B_k-1 that are linked together in which one tree becomes the left subtree of another binomial tree.

We can understand it with the example given below.

If B₀, where k is 0, there would exist only one node in the tree.

If B₁, where k is 1. Therefore, there would be two binomial trees of B₀ in which one B₀ becomes the left subtree of another B₀.

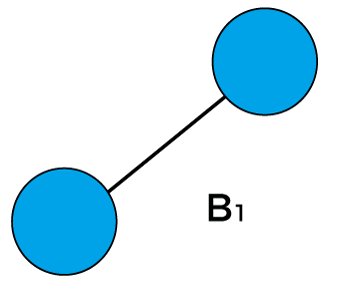
If B₂, where k is 2. Therefore, there would be two binomial trees of B₁ in which one B₁ becomes the left subtree of another B₁.

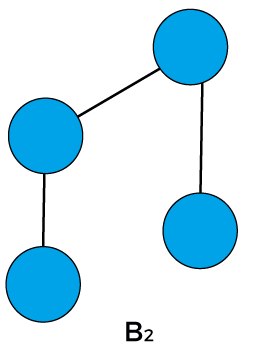
If B₃, where k is 3. Therefore, there would be two binomial trees of B₂ in which one B₂ becomes the left subtree of another B₂.

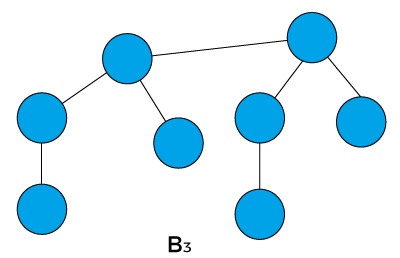
Now, let’s start the main topic ‘Binomial Heap’.

What is a Binomial Heap?

A binomial heap can be defined as the collection of binomial trees that satisfies the heap properties, i.e., min-heap. The min-heap is a heap in which each node has a value lesser than the value of its child nodes. Mainly, Binomial heap is used to implement a priority queue. It is an extension of binary heap that gives faster merge or union operations along with other operations provided by binary heap.

Properties of Binomial heap

There are following properties for a binomial heap with n nodes –

• Every binomial tree in the heap must follow the min-heap property, i.e., the key of a node is greater than or equal to the key of its parent.
• For any non-negative integer k, there should be atleast one binomial tree in a heap where root has degree k.

The first property of the heap ensures that the min-heap property is hold throughout the heap. Whereas the second property listed above ensures that a binary tree with n nodes should have at most 1 + log₂ n binomial trees, here log₂ is the binary logarithm.

We can understand the properties listed above with the help of an example –

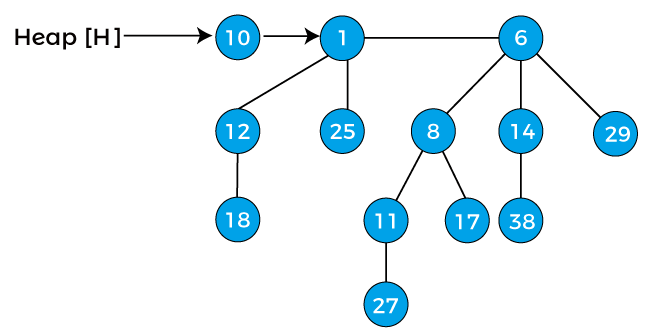
The above figure has three binomial trees, i.e., B₀, B₂, and B₃. The above all three binomial trees satisfy the min heap’s property as all the nodes have a smaller value than the child nodes.

The above figure also satisfies the second property of the binomial heap. For example, if we consider the value of k as 3, we can observe in the above figure that the binomial tree of degree 3 exists in a heap.

Binomial Heap and the binary representation of a number

A binomial heap with n nodes consists the binomial trees equal to the number of set bits in the binary representation of n.

Suppose we want to create the binomial heap of ‘n’ nodes that can be simply defined by the binary number of ‘n’. For example: if we want to create the binomial heap of 13 nodes; the binary form of 13 is 1101, so if we start the numbering from the rightmost digit, then we can observe that 1 is available at the 0, 2, and 3 positions; therefore, the binomial heap with 13 nodes will have B₀, B₂, and B₃ binomial trees.

We can use another example to understand it more clearly, suppose we have to create the binomial heap with 9 nodes. The binary representation of 9 is 1001. So, in the binary representation of 9, digit 1 is occurring at 0 and 3 positions, therefore, the binomial heap will contain the binomial trees of 0 and 3 degrees.

Now, let’s move towards the operations performed on Binomial heap.

Operations on Binomial Heap

The operations that can be performed on binomial heap are listed as follows –

• Creating a binomial heap
• Finding the minimum key
• Union or merging of two binomial heaps
• Inserting a node
• Extracting minimum key
• Decreasing a key
• Deleting a node

Now, let’s discuss the above-listed operations in detail.

Creating a new binomial heap

When we create a new binomial heap, it simply takes O(1) time because creating a heap will create the head of the heap in which no elements are attached.

Finding the minimum key

As stated above, binomial heap is the collection of binomial trees, and every binomial tree satisfies the min-heap property. It means that the root node contains a minimum value. Therefore, we only have to compare the root node of all the binomial trees to find the minimum key. The time complexity of finding the minimum key in binomial heap is O(logn).

Union or Merging of two binomial heap

It is the most important operation performed on the binomial heap. Merging in a heap can be done by comparing the keys at the roots of two trees, and the root node with the larger key will become the child of the root with a smaller key than the other. The time complexity for finding a union is O(logn). The function to merge the two trees is given as follows –

To perform the union of two binomial heaps, we have to consider the below cases –

Case 1: If degree[x] is not equal to degree[next x], then move pointer ahead.

Case 2: if degree[x] = degree[next x] = degree[sibling(next x)] then,

Move the pointer ahead.

Case 3: If degree[x] = degree[next x] but not equal to degree[sibling[next x]]

and key[x] < key[next x] then remove [next x] from root and attached to x.

Case 4: If degree[x] = degree[next x] but not equal to degree[sibling[next x]]

and key[x] > key[next x] then remove x from root and attached to [next x].

Now, let’s understand the merging or union of two binomial heaps with the help of an example. Consider two binomial heaps –

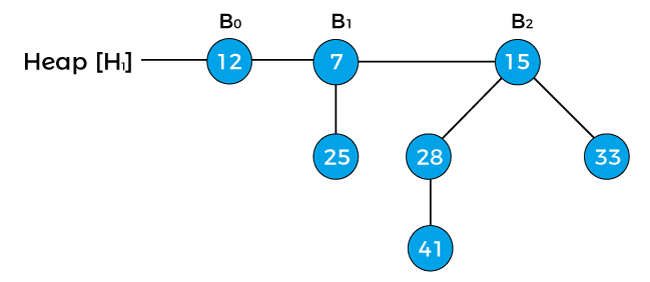
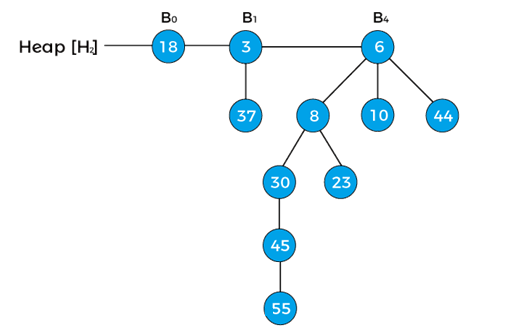
We can see that there are two binomial heaps, so, first, we have to combine both heaps. To combine the heaps, first, we need to arrange their binomial trees in increasing order.

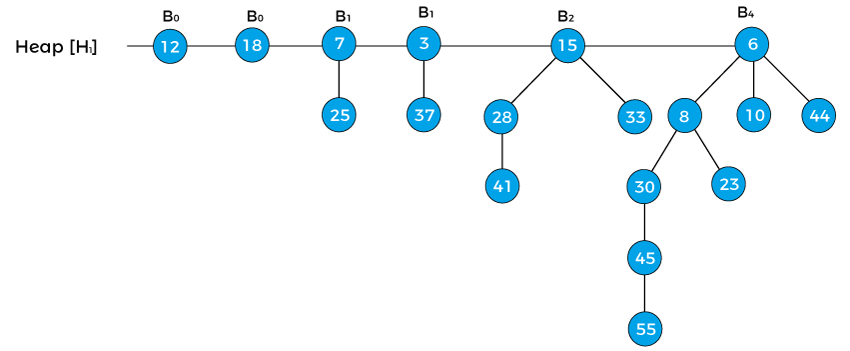
In the above heap first, the pointer x points to the node 12 with degree B₀, and the pointer next[x] points the node 18 with degree B₀. Node 7 with degree B₁ is the sibling of 18, therefore, it is represented as sibling[next[x]].

Now, first apply Case1 that says ‘if degree[x] ≠ degree[next x] then move pointer ahead’ but in the above example, the degree[x] = degree[next[x]], so this case is not valid.

Now, apply Case2 that says ‘if degree[x] = degree[next x] = degree[sibling(next x)] then Move pointer ahead’. So, this case is also not applied in the above heap.

Now, apply Case3 that says ‘ If degree[x] = degree[next x] ≠ degree[sibling[next x]] and key[x] < key[next x] then remove [next x] from root and attached to x’. We will apply this case because the above heap follows the conditions of case 3 –

degree[x] = degree[next x] ≠ degree[sibling[next x]] {as, B₀ = B₀¬ ≠ B₁} and key[x] < key[next x] {as 12 < 18}.

So, remove the node 18 and attach it to 12 as shown below –

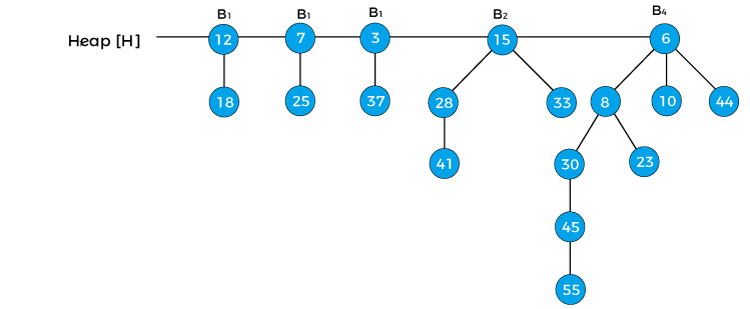
x = 12, next[x] = 7, sibling[next[x]] = 3, and degree[x] = B₁, dgree[next[x]] = B₁, degree[sibling[next[x]]] = B₁

Now we will reapply the cases in the above binomial heap. First, we will apply case 1. Since x is pointing to node 12 and next[x] is pointing to node 7, the degree of x is equal to the degree of next x; therefore, case 1 is not valid.

Here, case 2 is valid as the degree of x, next[x], and sibling[next[x]] is equal. So, according to the case, we have to move the pointer ahead.

Therefore, x = 7, next[x] = 3, sibling[next[x]] = 15, and degree[x] = B₁, dgree[next[x]] = B₁, degree[sibling[next[x]]] = B₂

Now, let’s try to apply case 3, here, first condition of case3 is satisfied as degree[x] = degree[next[x]] ≠ degree[sibling[next[x]]], but second condition (key[x] < key[next x]) of case 3 is not satisfied.

Now, let’s try to apply case 4. So, first condition of case4 is satisfied and second condition (key[x] > key[next x]) is also satisfied. Therefore, remove x from the root and attach it to [next[x]].

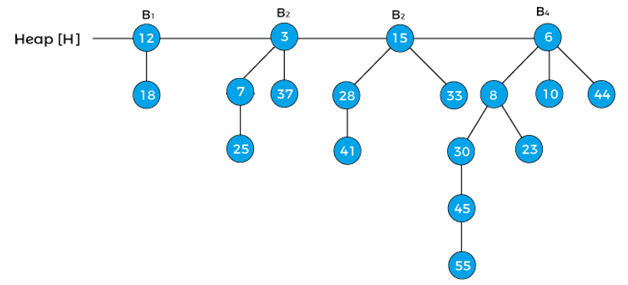
Now, the pointer x points to node 3, next[x] points to node 15, and sibling[next[x]] points to the node 6. Since, the degree of x is equal to the degree of next[x] but not equal to the degree[sibling[next[x]]], and the key value of x is less than the key value of next[x], so we have to remove next[x] and attach it to x as shown below –

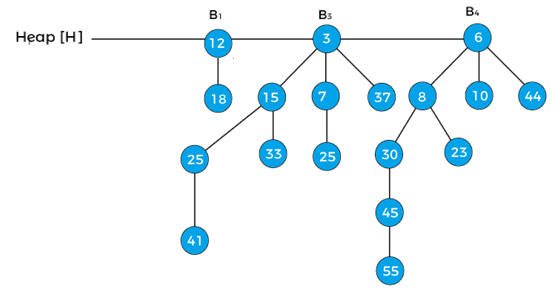
Now, x represents to the node 3, and next[x] points to node 6. Since, the degree of x and next[x] is not equal, so case1 is valid. Therefore, move the pointer ahead. Now, the pointer x points the node 6.

The B4 is the last binomial tree in a heap, so it leads to the termination of the loop. The above tree is the final tree after the union of two binomial heaps.

Insert an element in the heap

Inserting an element in the heap can be done by simply creating a new heap only with the element to be inserted, and then merging it with the original heap. Due to the merging, the single insertion in a heap takes O(logn) time. Now, let’s understand the process of inserting a new node in a heap using an example.

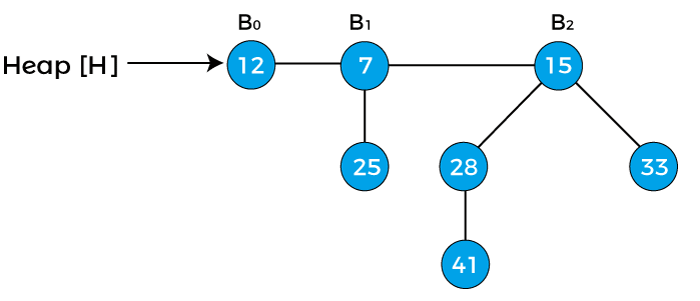
In the above heap, there are three binomial trees of degrees 0, 1, and 2 are given where B0 is attached to the head of the heap.

Suppose we have to insert node 15 in the above heap.

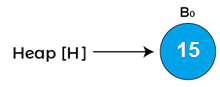
First, we have to combine both of the heaps. As both node 12 and node 15 are of degree 0, so node 15 is attached to node 12 as shown below –

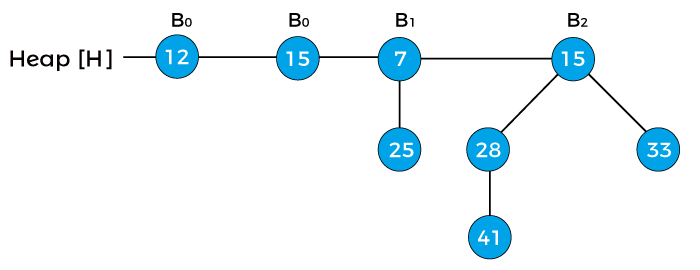
Now, assign x to B₀ with value 12, next(x) to B₀ with value 15, and assign sibling(next(x)) to B₁ with value 7. As the degree of x and next(x) is equal. The key value of x is smaller than the key value of next(x), so next(x) is removed and attached to the x. It is shown in the below image –

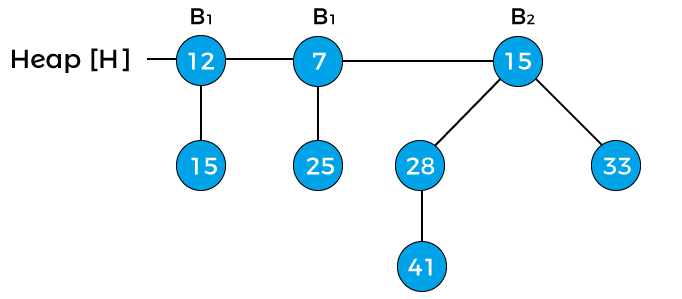
Now, x points to node 12 with degree B₁, next(x) to node 7 with degree B₁, and sibling(next(x)) points to node 15 with degree B₂. The degree of x is equal to the degree of next(x) but not equal to the degree of sibling(next(x)). The key value of x is greater than the key value of next(x); therefore, x is removed and attached to the next(x) as shown in the below image –

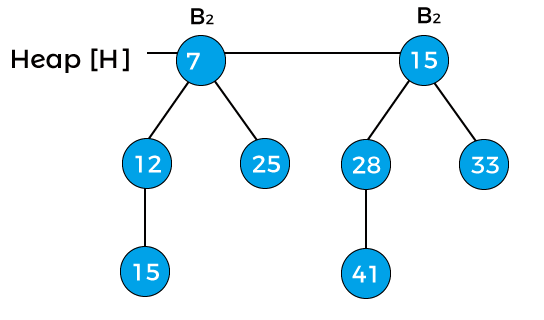
Now, x points to node 7, and next(x) points to node 15. The degree of both x and next(x) is B₂, and the key value of x is less than the key value of next(x), so next(x) will be removed and attached to x as shown in the below image –

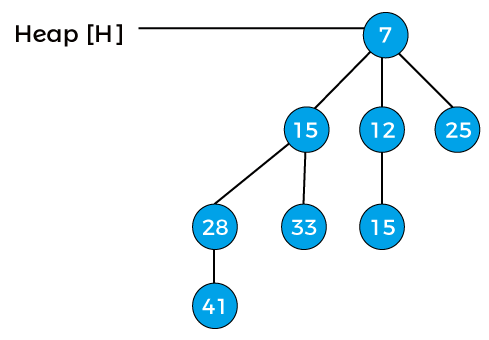
Now, the degree of the above heap is B₃, and it is the final binomial heap after inserting node 15.

Extracting the minimum key

It means that we have to remove an element with the minimum key value. As we know, in min-heap, the root element contains the minimum key value. So, we have to compare the key value of the root node of all the binomial trees. Let’s see an example of extracting the minimum key from the heap.

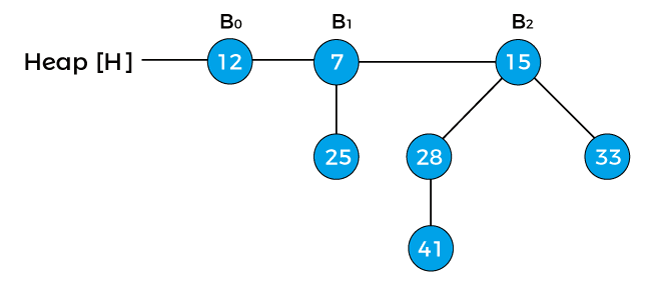
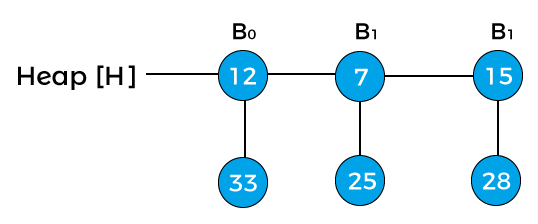
Suppose the heap is –

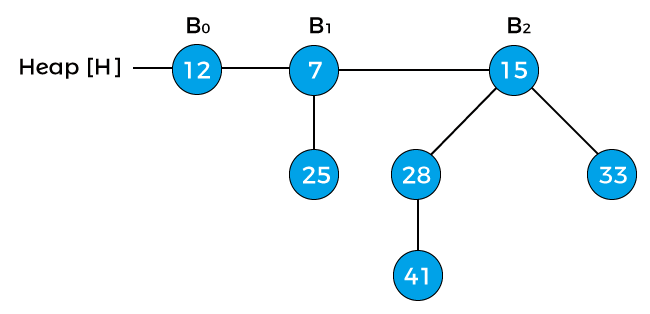
Now, compare the key values of the root node of the binomial trees in the above heap. So, 12, 7, and 15 are the key values of the root node in the above heap in which 7 is minimum; therefore, remove node 7 from the tree as shown in the below image –

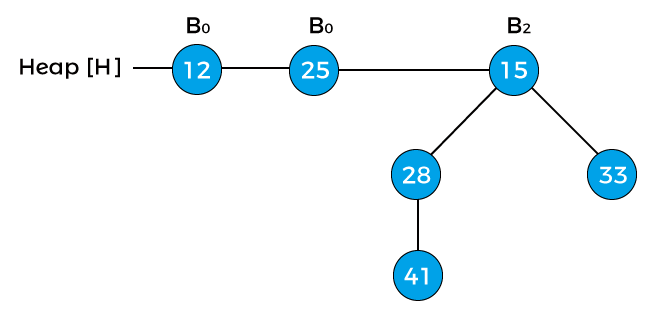
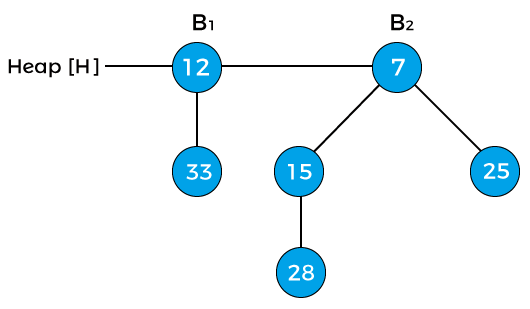
Now, the degree of node 12 and node 25 is B₀, and the degree of node 15 is B₂. Pointer x points to the node 12, next(x) points to the node 25, and sibling(next(x)) points to the node 15. Since the degree of x is equal to the degree of next(x) but not equal to the degree of sibling(next(x)). Value of pointer x is less than the pointer next(x), so node 25 will be removed and attached to node 12 as shown in the below image –

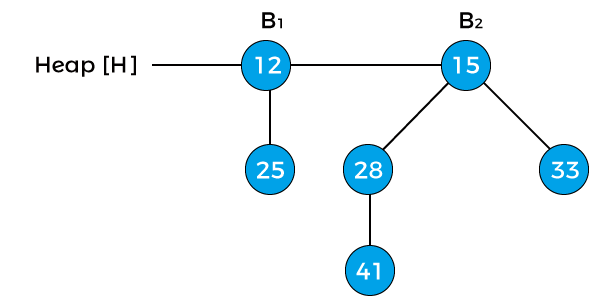
Now, the degree of node 12 is changed to B₁. The above heap is the final heap after extracting the minimum key.

Decreasing a key

Now, let’s move forward to another operation to be performed on binomial heap. Once the value of the key is decreased, it might be smaller than its parent’s key that results in the violation of min-heap property. If such case occurs after decreasing the key, then exchange the element with its parent, grandparent, and so on until the min-heap property is satisfied.

Let’s understand the process of decreasing a key in a binomial heap using an example. Consider a heap given below –

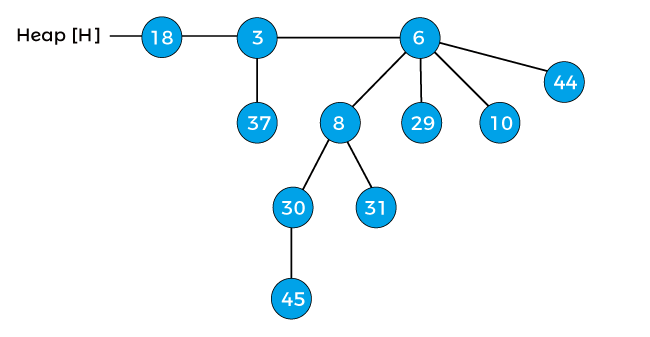
Decrease the key 45 by 7 of the above heap. After decreasing 45 by 7, the heap will be –

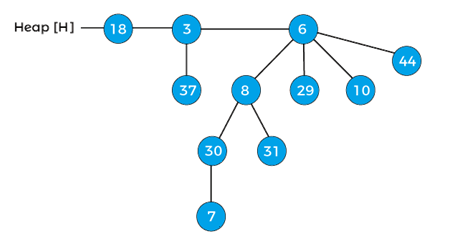
After decreasing the key, the min-heap property of the above heap is violated. Now, compare 7 wits its parent 30, as it is lesser than the parent, swap 7 with 30, and after swapping, the heap will be –

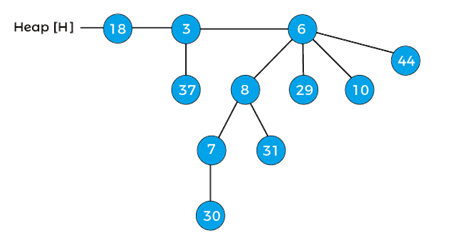
Again compare the element 7 with its parent 8, again it is lesser than the parent, so swap the element 7 with its parent 8, after swapping the heap will be –

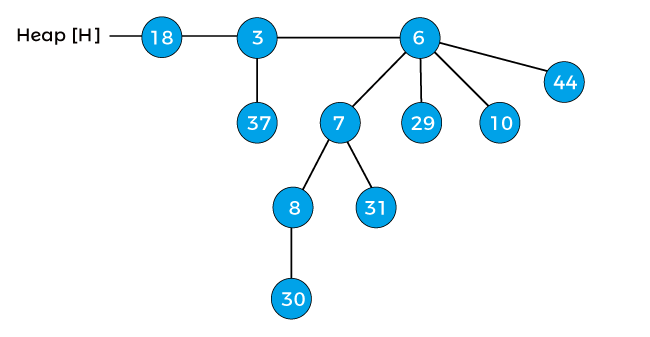
Now, the min-heap property of the above heap is satisfied. So, the above heap is the final heap after decreasing a key.

Deleting a node from the heap

To delete a node from the heap, first, we have to decrease its key to negative infinity (or -∞) and then delete the minimum in the heap. Now we will see how to delete a node with the help of an example. Consider the below heap, and suppose we have to delete the node 41 from the heap –

First, replace the node with negative infinity (or -∞) as shown below –

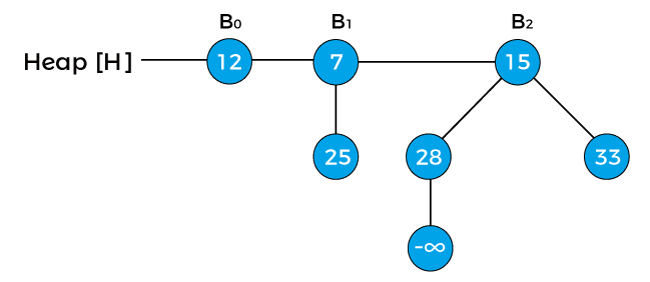
Now, swap the negative infinity with its root node in order to maintain the min-heap property.

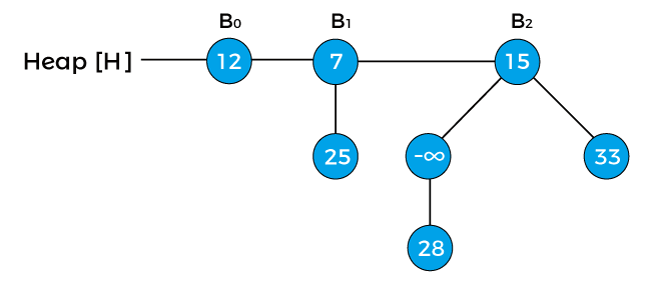
Now, again swap the negative infinity with its root node.

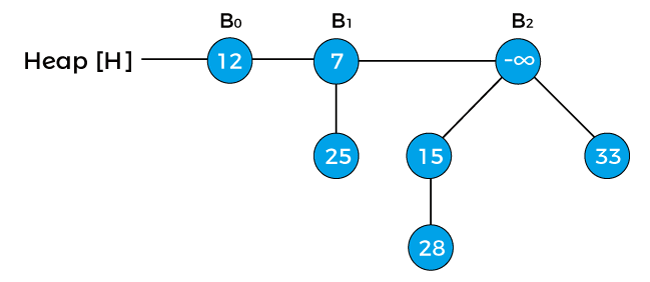
The next step is to extract the minimum key from the heap. Since the minimum key in the above heap is -infinity so we will extract this key, and the heap would be:

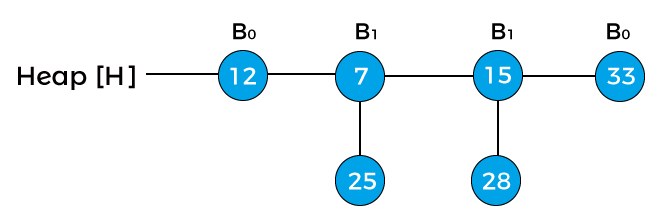
The above is the final heap after deleting the node 41.

Complexity of binomial heap

Now, let’s see the time complexity of the operations performed on binomial heap.

Time Complexity

Operations	Time complexity
Finding the minimum key	O(log n)
Inserting a node	O(log n)
Extracting minimum key	O(log n)
Decreasing a key	O(log n)
Union or merging	O(log n)
Deleting a node	O(log n)

The time complexity of finding the minimum element from the heap can be reduced to O(1). It can be done by using an additional pointer to the minimum element.

Space Complexity

The space complexity of a binomial heap with ‘n’ elements is O(n).

Conclusion

So, that’s all about the article. Here, we have discussed binomial heap along with its properties and complexity. We have also discussed the operations performed on binomial heap with the help of an example to make the topic easier to understand. Hope the article will be helpful and interesting to you.

---