Brute force approach
A brute force approach is an approach that finds all the possible solutions to find a satisfactory solution to a given problem. The brute force algorithm tries out all the possibilities till a satisfactory solution is not found.
Such an algorithm can be of two types:
- Optimizing: In this case, the best solution is found. To find the best solution, it may either find all the possible solutions to find the best solution or if the value of the best solution is known, it stops finding when the best solution is found. For example: Finding the best path for the travelling salesman problem. Here best path means that travelling all the cities and the cost of travelling should be minimum.
- Satisficing: It stops finding the solution as soon as the satisfactory solution is found. Or example, finding the travelling salesman path which is within 10% of optimal.
- Often Brute force algorithms require exponential time. Various heuristics and optimization can be used:
- Heuristic: A rule of thumb that helps you to decide which possibilities we should look at first.
- Optimization: A certain possibilities are eliminated without exploring all of them.
Let’s understand the brute force search through an example.
Suppose we have converted the problem in the form of the tree shown as below:
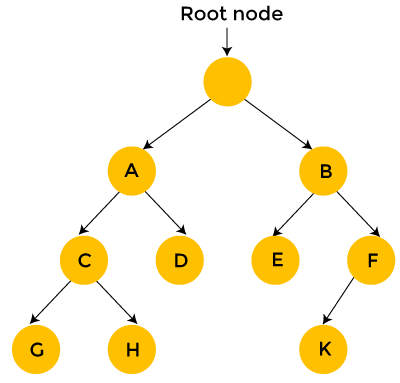
Brute force search considers each and every state of a tree, and the state is represented in the form of a node. As far as the starting position is concerned, we have two choices, i.e., A state and B state. We can either generate state A or state B. In the case of B state, we have two states, i.e., state E and F.
In the case of brute force search, each state is considered one by one. As we can observe in the above tree that the brute force search takes 12 steps to find the solution.
On the other hand, backtracking, which uses Depth-First search, considers the below states only when the state provides a feasible solution. Consider the above tree, start from the root node, then move to node A and then node C. If node C does not provide the feasible solution, then there is no point in considering the states G and H. We backtrack from node C to node A. Then, we move from node A to node D. Since node D does not provide the feasible solution, we discard this state and backtrack from node D to node A.
We move to node B, then we move from node B to node E. We move from node E to node K; Since k is a solution, so it takes 10 steps to find the solution. In this way, we eliminate a greater number of states in a single iteration. Therefore, we can say that backtracking is faster and more efficient than the brute force approach.
Advantages of a brute-force algorithm
The following are the advantages of the brute-force algorithm:
- This algorithm finds all the possible solutions, and it also guarantees that it finds the correct solution to a problem.
- This type of algorithm is applicable to a wide range of domains.
- It is mainly used for solving simpler and small problems.
- It can be considered a comparison benchmark to solve a simple problem and does not require any particular domain knowledge.
Disadvantages of a brute-force algorithm
The following are the disadvantages of the brute-force algorithm:
- It is an inefficient algorithm as it requires solving each and every state.
- It is a very slow algorithm to find the correct solution as it solves each state without considering whether the solution is feasible or not.
- The brute force algorithm is neither constructive nor creative as compared to other algorithms.
