Bubble sort vs. Selection sort
Here we will look at the differences between the selection sort and bubble sort. Before understanding the differences, we should know about the selection sort and bubble sort individually.
What is selection sort?
Sorting means arranging the elements of an array in ascending order. Selection sort is one sorting technique used for sorting the array. In selection sort, an array is divided into two sub- arrays, i.e., one is an unsorted sub-array, and the other is sorted sub-array. Initially, we assume that the sorted subarray is empty. First, we will find the minimum element from the unsorted subarray, and we will swap the minimum element with an element which is at the beginning position of the array. This algorithm is named as selection sort because it is selecting the minimum element and then performs swapping.
Let’s understand the selection sort through an example.

As we can observe in the above array that it contains 6 elements. The above array is an unsorted array whose indexing starts from 0 and ends at 5. The following are the steps used to sort the array:
Step 1: In the above array, the minimum element is 1; swap element 1 with an element 7.
Now, the sorted array contains only one element, i.e., 1, while the unsorted array contains 5
elements, i.e., 4, 10, 8, 3, 7.
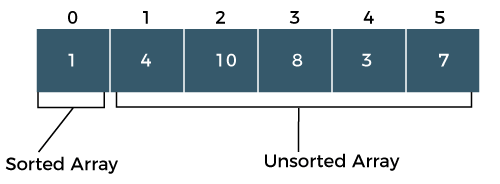
Step 2: In the unsorted sub-array, the minimum element is 3, so swap element 3 with an element 4, which is at the beginning of the unsorted sub-array.
Now the sorted array contains two elements, i.e., 1 and 3, while the unsorted array has four elements, i.e., 10, 8, 4, 7, as shown in the above figure.
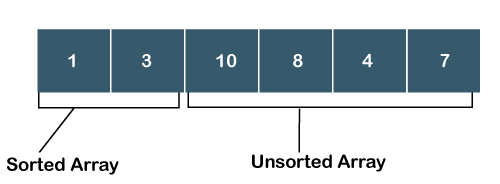
Step 3: Search the minimum element in the unsorted sub-array, and the minimum element is 4. Swap the element 4 with an element 10, which is at the beginning of the unsorted sub- array.
Now, the sorted array contains three elements, i.e., 1, 3, 4, while the unsorted array has three elements, i.e., 10, 8, 7
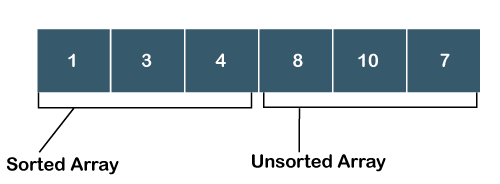
Step 4: Search the minimum element in the unsorted array, and the minimum element is 7. Swap element 7 with an element 10, which is at the beginning of the unsorted sub-array.
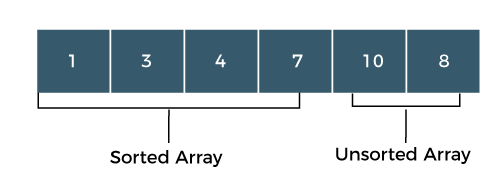
Now, the sorted array contains four elements, i.e., 1, 3, 4, 7, while the unsorted array has two elements, i.e., 10, 8.
Step 5: Search the minimum element in the unsorted array and the minimum element is 8. Swap the element 8 with an element 10 which is at the beginning of the unsorted sub-array.
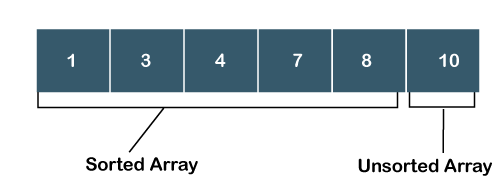
Now, the sorted array contains the elements, i.e., 1, 3, 4, 7, 8.
Step 6: The last element is left in the unsorted sub-array. Move the last element to the sorted sub array shown as below:
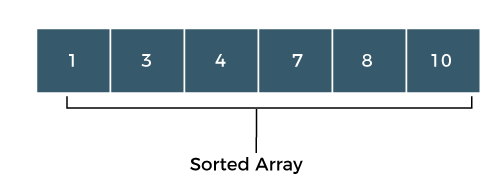
What is Bubble sort?
The bubble sort is also one of the sorting techniques used for sorting the elements of an array. The basic principle behind the bubble sort is that the two adjacent elements are to be compared; if those elements are in correct order, then we move to the next iteration. Otherwise, we swap those two elements. Let’s understand the bubble sort through an example.
Consider the below array:
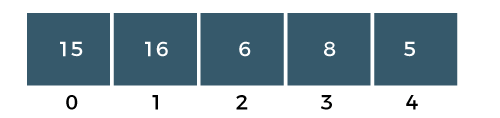
The above array is an unsorted array. An array consists of 5 integers, i.e., 15, 16, 6, 8, 5.
The following are the steps required used to sort the array:
PASS 1
Step 1: The a[0] element is compared with a a[1] element. The a[0] is less than a[1], i.e., 15<16, so no swapping would be done as shown in the below figure:
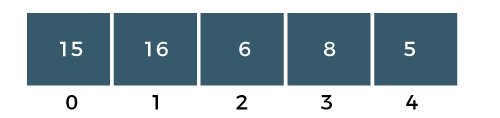
Step 2: Now, a[1] would be compared with a a[2] element. Since a[1] is greater than the a[0] element, i.e., 16>6, so swap 16 and 6 as shown in the below figure:
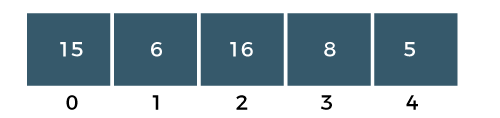
Step 3: The a[2] would be compared with a a[3] element. Since a[2] is greater than the a[3] element, i.e., 16>8, so swap 16 and 8 elements as shown in the below figure:
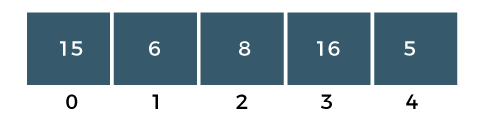
Step 4: The a[3] would be compared with a[4] element. Since a[3] is greater than the a[4], i.e., 16 > 5, so swap 16 and 5 elements as shown in the below figure:
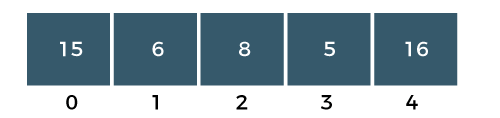
As we can observe in the above array that the element which is the largest has been bubbled up to its correct position. In other words, we can say that the largest element has been placed at the last position of the array. The above steps are included in PASS 1in which the largest element is at its correct position.
We will again start comparing the elements from the first position in PASS 2.
PASS 2:
Step 1: First, we compare a[0] with a[1] element. Since a[0] element is greater than the a[1] element, i.e., 15 > 6, swap a[0] element with a[1] as shown in the below figure:
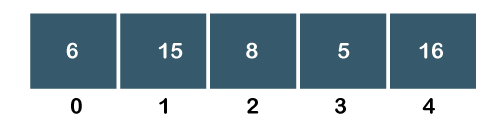
Step 2: The a[1] element would be compared with a[2] element. The a[1] is greater than the a[2], i.e., 15 > 8, so swap a[1] with element a[2] as shown in the below figure:
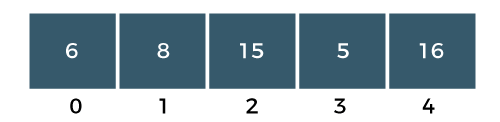
Step 3: The a[2] element would be compared with a a[3] element. Since a[2] is greater than the a[3] element, i.e., 15 > 5, swap element 15 with element 5 as shown in the below figure:
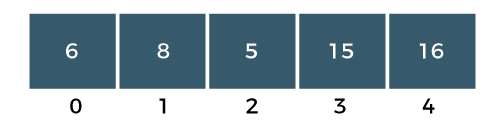
Step 4: Now, a[3] is compared to a[4]. Since a[3] is less than a[4], so no swapping would be done as shown in the below figure:
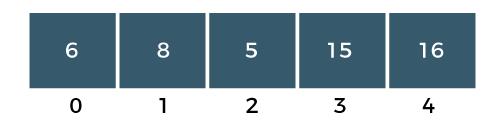
As we can observe above that the two elements are at the right position, largest (16) and the second largest element (15). In an array, three elements are unsorted, so again we will follow the same steps in PASS 3.
PASS 3:
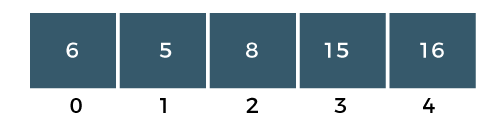
Step 1: First, we compare a[0] with a[1]. Since a[0] is less than a[1], i.e., 6 < 8, so no swapping would be done as shown in the below figure:
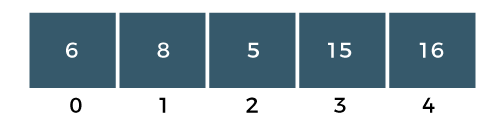
Step 2: Now, a[1] would be compared with a[2]. As a[1] is greater than a[2], so swap the element 8 with the element 5 as shown in the below figure:
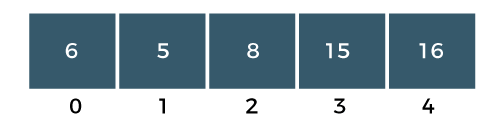
Step 3: The a[2] would be compared with a[3]. Since a[2] is less than a[3], i.e., 8 < 15, so no swapping would be done as shown in the below figure:
Step 4: The a[3] element would be compared with a[4]. Since a[3] is less than a[4], i.e., 15 < 16, so no swapping would be done as shown in the below figure:
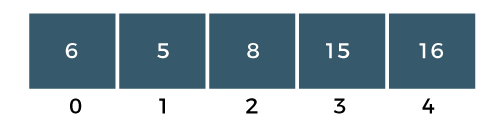
In PASS 3, three elements are at the right positions, largest, second largest and third largest. In an array, two elements are not sorted, so again we will follow the same steps in PASS 4.
PASS 4:
Step 1: First, we will compare a[0] and a[1]. Swap the a[0] with a[1] as a[0] is greater than a[1].
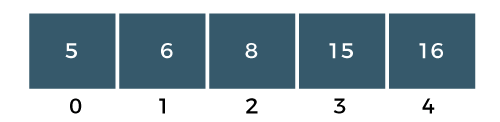
The above array is a sorted array as all the elements are at the correct positions.
Differences between Bubble sort and Selection sort

| Bubble sort | Selection sort |
|---|---|
| In bubble sort, two adjacent elements are compared. If the adjacent elements are not at the correct position, swapping would be performed. | In selection sort, the minimum element is selected from the array and swap with an element which is at the beginning of the unsorted sub array. |
| The time complexities in best case and worst case are O(n) and O(n2) respectively. | The time complexity in both best and worst cases is O(n 2). |
| It is not an efficient sorting technique. | It is an efficient sorting technique as compared to Bubble sort. |
| It uses an exchanging method. | It uses a selection method. |
| It is slower than the selection sort as a greater number of comparisons is required. | It is faster than the bubble sort as a lesser number of comparisons is required. |
