Aptitude Calendar Concepts and Formulas
Points to remember:
1. Problems on calendar mainly deal with finding the day of the week on a given date using the number of odd days.
2. Odd days: Odd days are different from odd numbers. They are the number of days more than the complete number of weeks in a given period.
3. To find the number of odd days divide the given number of by seven. The remainder left represents the number of odd days.
For example: if the given number of days is 80, after dividing 80 by 7, the remainder left is 3. Hence, there are three odd days.
Similarly, if the given number of days is 77, after dividing 77 by 7, the remainder left is 0. Hence, there are 0 odd days.
4. Ordinary year: A year which is not a leap year is called an ordinary year. It has 365 days.
5. Leap year: A year which is divisible by 4 is called a leap year, e.g. 1992, 1996, 2000, etc., are leap years. A leap year has 366 days. If the year is a century, it will be a leap year if it is divisible by 400, i.e. every 4th century is a leap year, e.g. 400, 800, 1200, etc., but 200, 500, 1900, etc., are not leap years.
Counting odd:
Odd days in an ordinary year: An ordinary year contains 365 days. On dividing 365 by 7, we get 1 as a remainder (52*7 +1) or (52 weeks + 1 day). It means an ordinary year has one odd day.
Odd days in a leap year: A leap year contains 366. On dividing 366 by 7, we get 2 as remainder (52*7 + 2) or (52 weeks + 2). It means a leap year has two odd days.
Odd days in a century: A century has 76 ordinary years and 24 leap years.
∴100 years = 76 ordinary years + 24 leap years
= [(76*52) weeks + 76 odd days] + [(24*52) weeks + 48 odd days]
= [(100*52) weeks + 124 odd days]
= (5200 weeks + 17 weeks + 5 odd days)
= (5217 weeks + 5 odd days)
∴A century or 100 years have 5 odd days.
Similarly, in 200 years, there will be 10 (5+5) days, 7 days (1 week) + 3 odd days. So, 200 years have 3 odd days.
In 300 years, there will be 15 days, 14 days (2 weeks) + 1 odd day. So, 300 years have 1 odd day.
In 400 years, there will be 20 + 1(as 400 is a leap year) = 21 days, 21 days (3 weeks). So, 400 years have 0 odd days. A century divisible by 400 also has 0 odd days.
Tables of odd :
a.) Table showing the relation between the year and the number of odd ;
| Years | No. of odd |
|---|---|
| Ordinary year | 1 |
| Leap year | 2 |
| 100 years | 5 |
| 200 years | 3 |
| 300 years | 1 |
| 400 years | 0 |
b.) Table showing the relation between the day of the week and the number of odd ;
| Day of week | No. of odd |
|---|---|
| Sunday | 0 |
| Monday | 1 |
| Tuesday | 2 |
| Wednesday | 3 |
| Thursday | 4 |
| Friday | 5 |
| Saturday | 6 |
Notes:
- The years which are divisible by 400 have 0 odd days, e.g. 400, 800, 1200, 1600, 2000, etc.
- Last day of a century cannot be Tuesday, Thursday or Saturday.
- April & July for all years and January and October for non-leap years have the same calendar.
- The calendars of two different years are same if they satisfy the following conditions;
a) The years must be of the same type, i.e. both must be either ordinary years or leap years.
b) January 21 of both the years, must be the same day of the week.
The leap years in the 20th and 21st centuries;
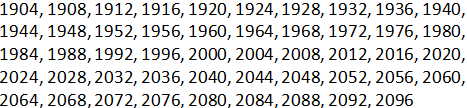
Aptitude Calendar Test Paper 1
Aptitude Calendar Test Paper 2
