Chromatic Number of graphs | Graph coloring in Graph theory
Graph coloring
Graph coloring can be described as a process of assigning colors to the vertices of a graph. In this, the same color should not be used to fill the two adjacent vertices. We can also call graph coloring as Vertex Coloring. In graph coloring, we have to take care that a graph must not contain any edge whose end vertices are colored by the same color. This type of graph is known as the Properly colored graph.
Example of Graph coloring
In this graph, we are showing the properly colored graph, which is described as follows:
The above graph contains some points, which are described as follows:
- The same color cannot be used to color the two adjacent vertices.
- Hence, we can call it as a properly colored graph.
Applications of Graph coloring
There are various applications of graph coloring. Some of their important applications are described as follows:
- Assignment
- Map coloring
- Scheduling the tasks
- Sudoku
- Prepare time table
- Conflict resolution
Chromatic Number
The chromatic number can be described as the minimum number of colors required to properly color any graph. In other words, the chromatic number can be described as a minimum number of colors that are needed to color any graph in such a way that no two adjacent vertices of a graph will be assigned the same color.
Example of Chromatic number:
To understand the chromatic number, we will consider a graph, which is described as follows:
The above graph contains some points, which are described as follows:
- The same color is not used to color the two adjacent vertices.
- The minimum number of colors of this graph is 3, which is needed to properly color the vertices.
- Hence, in this graph, the chromatic number = 3
- If we want to properly color this graph, in this case, we are required at least 3 colors.
Types of Chromatic Number of Graphs:
There are various types of chromatic number of graphs, which are described as follows:
Cycle Graph:
A graph will be known as a cycle graph if it contains ‘n’ edges and ‘n’ vertices (n >= 3), which form a cycle of length ‘n’. There can be only 2 or 3 number of degrees of all the vertices in the cycle graph.
Chromatic number:
- The chromatic number in a cycle graph will be 2 if the number of vertices in that graph is even.
- The chromatic number in a cycle graph will be 3 if the number of vertices in that graph is odd.
Examples of Cycle graph:
There are various examples of cycle graphs. Some of them are described as follows:
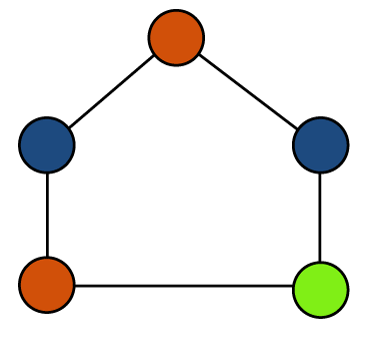
Example 1: In the following graph, we have to determine the chromatic number.
Solution: In the above cycle graph, there are 3 different colors for three vertices, and none of the adjacent vertices are colored with the same color. In this graph, the number of vertices is odd. So
Chromatic number = 3
Example 2: In the following graph, we have to determine the chromatic number.
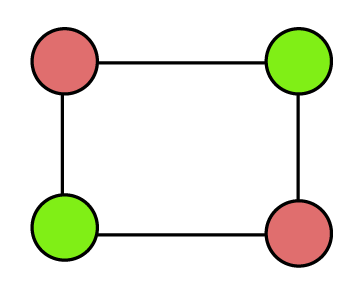
Solution: In the above cycle graph, there are 2 colors for four vertices, and none of the adjacent vertices are colored with the same color. In this graph, the number of vertices is even. So
Chromatic number = 2
Example 3: In the following graph, we have to determine the chromatic number.
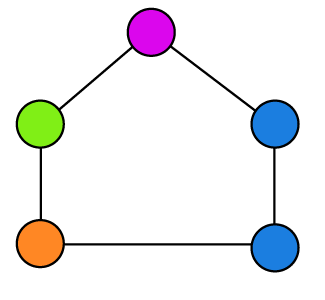
Solution: In the above graph, there are 4 different colors for five vertices, and two adjacent vertices are colored with the same color (blue). So this graph is not a cycle graph and does not contain a chromatic number.
Example 4: In the following graph, we have to determine the chromatic number.
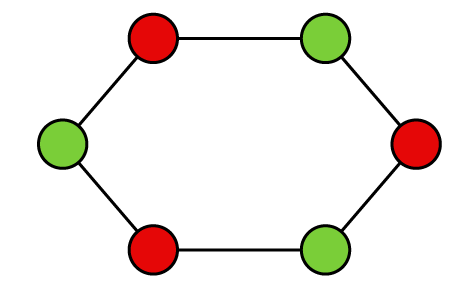
Solution: In the above graph, there are 2 different colors for six vertices, and none of the adjacent vertices are colored with the same color. In this graph, the number of vertices is even. So
Chromatic number = 2
Planner Graph
A graph will be known as a planner graph if it is drawn in a plane. The edges of the planner graph must not cross each other.
Chromatic Number:
- In a planner graph, the chromatic Number must be Less than or equal to 4.
- The planner graph can also be shown by all the above cycle graphs except example 3.
Examples of Planer graph:
There are various examples of planer graphs. Some of them are described as follows:
Example 1: In the following graph, we have to determine the chromatic number.
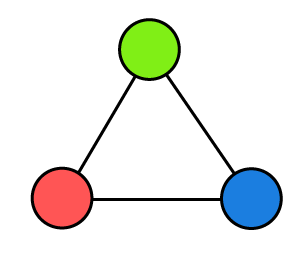
Solution: In the above graph, there are 3 different colors for three vertices, and none of the edges of this graph cross each other. So
Chromatic number = 3
Here, the chromatic number is less than 4, so this graph is a plane graph.
Example 2: In the following graph, we have to determine the chromatic number.
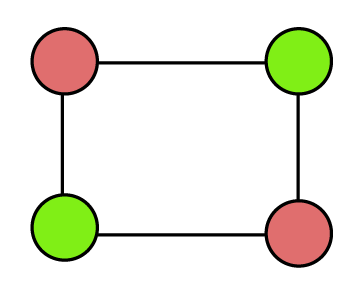
Solution: In the above graph, there are 2 different colors for four vertices, and none of the edges of this graph cross each other. So
Chromatic number = 2
Here, the chromatic number is less than 4, so this graph is a plane graph.
Example 3: In the following graph, we have to determine the chromatic number.
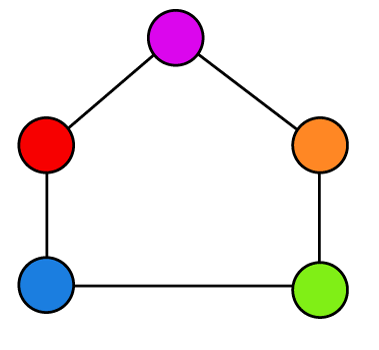
Solution: In the above graph, there are 5 different colors for five vertices, and none of the edges of this graph cross each other. So
Chromatic number = 5
Here, the chromatic number is greater than 4, so this graph is not a plane graph.
Example 4: In the following graph, we have to determine the chromatic number.
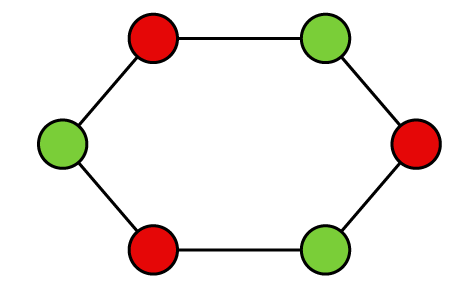
Solution: In the above graph, there are 2 different colors for six vertices, and none of the edges of this graph cross each other. So
Chromatic number = 2
Here, the chromatic number is less than 4, so this graph is a plane graph.
Complete Graph
A graph will be known as a complete graph if only one edge is used to join every two distinct vertices. Every vertex in a complete graph is connected with every other vertex. In this graph, every vertex will be colored with a different color. That means in the complete graph, two vertices do not contain the same color.
Chromatic Number
In a complete graph, the chromatic number will be equal to the number of vertices in that graph.
Examples of Complete graph:
There are various examples of complete graphs. Some of them are described as follows:
Example 1: In the following graph, we have to determine the chromatic number.
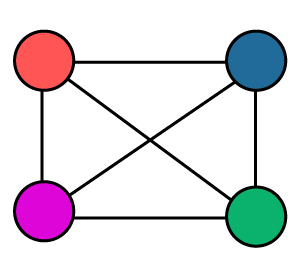
Solution: There are 4 different colors for 4 different vertices, and none of the colors are the same in the above graph. According to the definition, a chromatic number is the number of vertices. So,
Chromatic number = 4
Example 2: In the following graph, we have to determine the chromatic number.
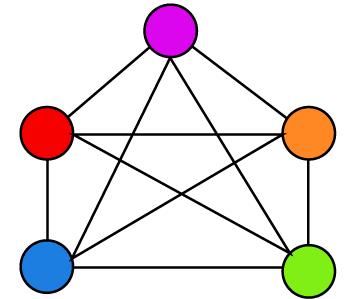
Solution: There are 5 different colors for 5 different vertices, and none of the colors are the same in the above graph. According to the definition, a chromatic number is the number of vertices. So,
Chromatic number = 5
Example 3: In the following graph, we have to determine the chromatic number.
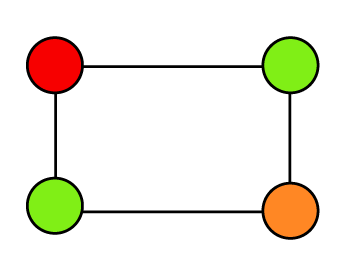
Solution: There are 3 different colors for 4 different vertices, and one color is repeated in two vertices in the above graph. So this graph is not a complete graph and does not contain a chromatic number.
Bipartite Graph
A graph will be known as a bipartite graph if it contains two sets of vertices, A and B. The vertex of A can only join with the vertices of B. That means the edges cannot join the vertices with a set.
Chromatic Number
In any bipartite graph, the chromatic number is always equal to 2.
Examples of Bipartite graph:
There are various examples of bipartite graphs. Some of them are described as follows:
Example 1: In the following graph, we have to determine the chromatic number.
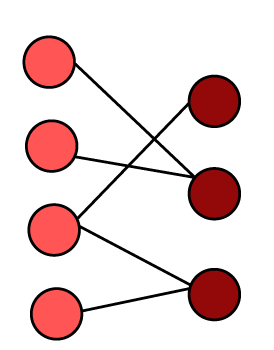
Solution: There are 2 different sets of vertices in the above graph. So the chromatic number of all bipartite graphs will always be 2. So
Chromatic number = 2
Tree:
A connected graph will be known as a tree if there are no circuits in that graph. In a tree, the chromatic number will equal to 2 no matter how many vertices are in the tree. Every bipartite graph is also a tree.
Chromatic Number
In any tree, the chromatic number is equal to 2.
Examples of Tree:
There are various examples of a tree. Some of them are described as follows:
Example 1: In the following tree, we have to determine the chromatic number.
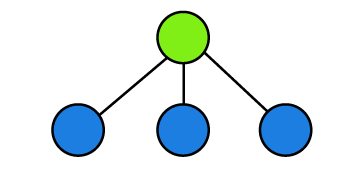
Solution: There are 2 different colors for four vertices. A tree with any number of vertices must contain the chromatic number as 2 in the above tree. So,
Chromatic number = 2
Example 2: In the following tree, we have to determine the chromatic number.
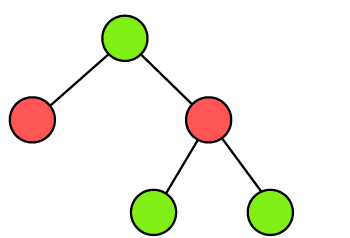
Solution: There are 2 different colors for five vertices. A tree with any number of vertices must contain the chromatic number as 2 in the above tree. So,
Chromatic number = 2
Real-life example of Chromatic Number
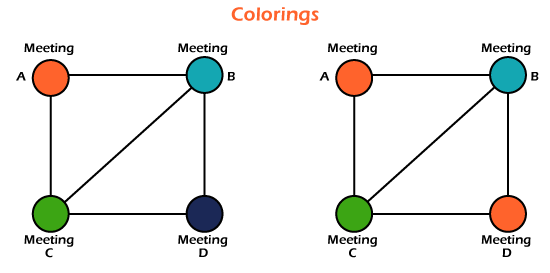
Suppose Marry is a manager in Xyz Company. The company hires some new employees, and she has to get a training schedule for those new employees. She has to schedule the three meetings, and she is trying to use the few time slots as much as possible for meetings. If there is an employee who has to be at two different meetings, then the manager needs to use the different time schedules for those meetings. Suppose we want to get a visual representation of this meeting.
For the visual representation, Marry uses the dot to indicate the meeting. If there is an employee who has two meetings and requires to join both the meetings, then both the meeting will be connected with the help of an edge. The different time slots are represented with the help of colors. So the manager fills the dots with these colors in such a way that two dots do not contain the same color that shares an edge. (That means an employee who needs to attend the two meetings must not have the same time slot). The visual representation of this is described as follows: