Comb Sort Algorithm

In this article, we will discuss the comb sort Algorithm. Comb Sort is the advanced form of bubble Sort. Bubble Sort compares all the adjacent values while comb sort removes all the turtle values or small values near the end of the list.

It is a comparison-based sorting algorithm that is mainly an improvement in bubble sort. In bubble sort, there is a comparison between the adjacent elements to sort the given array. So, in bubble sort, the gap size between the elements that are compared is 1. Comb sort improves the bubble sort by using a gap of size more than 1. The gap in the comb sort starts with the larger value and then shrinks by a factor of 1.3. It means that after the completion of each phase, the gap is divided by the shrink factor 1.3. The iteration continues until the gap is 1.

The shrink factor is found to be 1.3 by testing comb sort on 200,000 random lists. Comb sort works better than the bubble sort, but its time complexity in average case and worst case remains O(n²).

The process of performing the comb sort is given as follows –

STEP 1 START

STEP 2 Calculate the gap value if gap value==1 goto step 5 else goto step 3

STEP 3 Iterate over data set and compare each item with gap item then goto step 4.

STEP 4 Swap the element if require else goto step 2

STEP 5 Print the sorted array.

STEP 6 STOP

Now, let’s see the algorithm of comb sort.

Algorithm

  combSort(array, n) // n is the size of array    gap = n // Initialize gap size equal to the size of array    shrink = 1.3 // gap shrink factor    swapped = true  while (gap ! = 1 || swapped = true)  gap = floor(gap/1.3);  if gap ≤ 1      gap = 1  end if  swapped = false     for every element range from 0 to n-gap, do the following –          if array[i] > array[i+gap]  swap(array[i], array[i+gap])  swapped = true          end if  end for loop  end while loop  end combSort  

Working of comb Sort Algorithm

Now, let’s see the working of the comb sort Algorithm.

To understand the working of the comb sort algorithm, let’s take an unsorted array. It will be easier to understand the comb sort via an example.

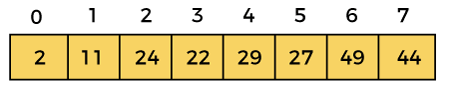
Let the elements of array are –

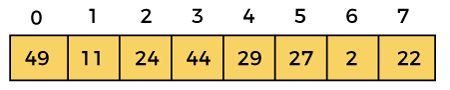
Now, initialize

n = 8 // size of array

gap = n

shrink = 1.3

swapped = true

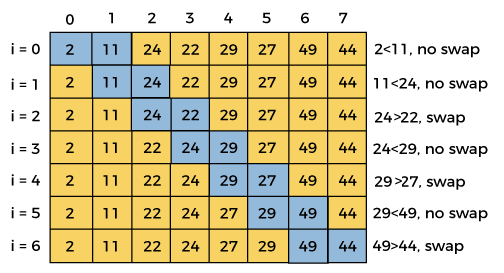
First iteration

gap = floor(gap/shrink) = floor(8/1.3) = 6

swapped = false

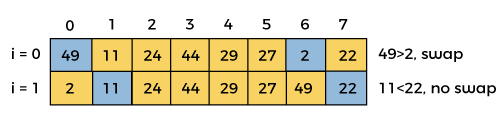
This iteration ends here, because at i =2, the value of i + gap = 2 + 6 = 8, and there is no element at 8^th position of the array. So, after first iteration, the elements of array will be –

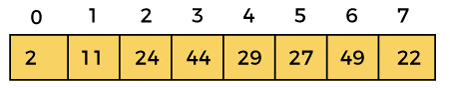
Now, move to iteration 2.

Second iteration

gap = floor(gap/shrink) = floor(6/1.3) = 4

swapped = false

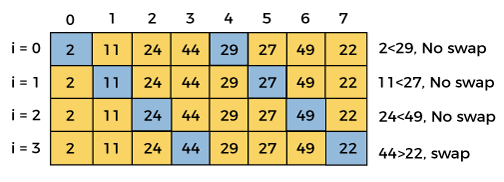
This iteration ends here, because at i =4, the value of i + gap = 4 + 4 = 8, and there is no element at 8^th position of the array. So, after second iteration, the elements of array will be –

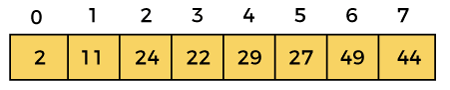
Now, move to iteration 3.

Third iteration

gap = floor(gap/shrink) = floor(4/1.3) = 3

swapped = false

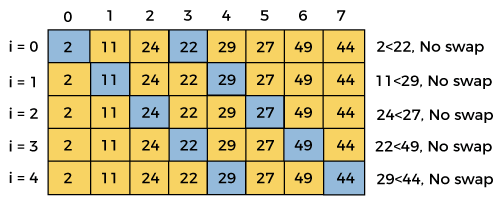
This iteration ends here, because at i =5, the value of i + gap = 5 + 3 = 8, and there is no element at 8^th position of the array. So, after third iteration, the elements of array will be –

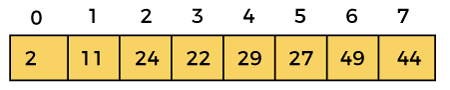
Now, move to iteration 4.

Fourth iteration

gap = floor(gap/shrink) = floor(3/1.3) = 2

swapped = false

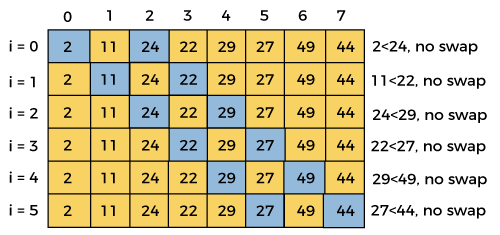
This iteration ends here, because at i =6, the value of i + gap = 6 + 2 = 8, and there is no element at 8^th position of the array. So, after fourth iteration, the elements of array will be –

Now, move to iteration 5.

Fifth iteration

gap = floor(gap/shrink) = floor(2/1.3) = 1

swapped = false

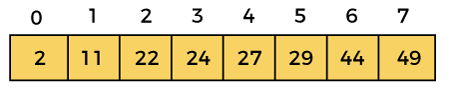
After the fifth iteration, the sorted array is –

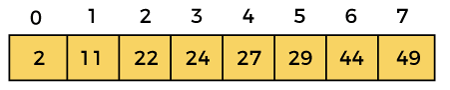
Hence, the iterations end here, and now the sorting is completed. Now, the final sorted array is –

Comb sort complexity

Now, let’s see the time complexity of Comb sort in the best case, average case, and worst case. We will also see the space complexity of Comb sort.

1. Time Complexity

Case	Time Complexity
Best Case	θ(n log n)
Average Case	Ω(n²/2^p) where p is a number of increments.
Worst Case	O(n²)

Best Case Complexity – It occurs when there is no sorting required, i.e. the array is already sorted. The best-case time complexity of comb sort is θ(n log n).
Average Case Complexity – It occurs when the array elements are in jumbled order that is not properly ascending and not properly descending. The average case time complexity of comb sort is Ω(n²/2^p), where p is a number of increments..
Worst Case Complexity – It occurs when the array elements are required to be sorted in reverse order. That means suppose you have to sort the array elements in ascending order, but its elements are in descending order. The worst-case time complexity of comb sort is O(n²).

2. Space Complexity

Space Complexity	O(1)
Stable	YES

The space complexity of comb sort is O(1).

Implementation of Comb sort

Now, let’s see the programs of Comb sort in different programming languages.

Program: Write a program to implement comb sort in C language.

  #include   #include    int updatedGap(int gap)  {  // Shrink gap by Shrink factor  gap = floor(gap/1.3);    if (gap < 1)  return 1;  return gap;  }      // Function to sort array elements using Comb Sort  void combSort(int a[], int n)  {  int gap = n; /* Initialize gap size equal to the size of array */    int swapped = 1;    while (gap != 1 || swapped == 1)  {  gap = updatedGap(gap); // find updated gap  // Initialize swapped as false so that we can  // check if swap happened or not  swapped = 0;    for (int i = 0; i < n-gap; i++) /* Compare all elements with current gap */  {  if (a[i] > a[i+gap]) //swap a[i] with a[i+gap]  {      int temp = a[i];                    a[i] = a[i+gap];                    a[i+gap] = temp;    swapped = 1;  }  }  }  }  void printArr(int a[], int n) /* function to print array elements */  {      for (int i=0; i;>

Output

Program: Write a program to implement comb sort in C++.

  #include   #include  using namespace std;    int updatedGap(int gap)  {  // Shrink gap by Shrink factor  gap = floor(gap/1.3);    if (gap < 1)  return 1;  return gap;  }    // Function to sort array elements using Comb Sort  void combSort(int a[], int n)  {  int gap = n; /* Initialize gap size equal to the size of array */    int swapped = 1;    while (gap != 1 || swapped == 1)  {  gap = updatedGap(gap); // find updated gap  // Initialize swapped as false so that we can  // check if swap happened or not  swapped = 0;    for (int i = 0; i < n-gap; i++) /* Compare all elements with current gap */  {  if (a[i] > a[i+gap]) //swap a[i] with a[i+gap]  {      int temp = a[i];                    a[i] = a[i+gap];                    a[i+gap] = temp;    swapped = 1;  }  }  }  }  void printArr(int a[], int n) /* function to print array elements */  {      for (int i=0; i;>

Output

Program: Write a program to implement comb sort in C#.

  using System;  class CombSort {  static int updatedGap(int gap)  {  // Shrink gap by Shrink factor  gap = (gap*10)/13;    if (gap < 1)  return 1;  return gap;  }    // Function to sort array elements using Comb Sort  static void combSort(int[] a, int n)  {  int gap = n; /* Initialize gap size equal to the size of array */    int swapped = 1;    while (gap != 1 || swapped == 1)  {  gap = updatedGap(gap); // find updated gap  // Initialize swapped as false so that we can  // check whether swap happened or not  swapped = 0;    for (int i = 0; i < n-gap; i++) /* Compare all elements with current gap */  {  if (a[i] > a[i+gap]) //swap a[i] with a[i+gap]  {      int temp = a[i];                    a[i] = a[i+gap];                    a[i+gap] = temp;    swapped = 1;  }  }  }  }  static void printArr(int[] a, int n) /* function to print array elements */  {      for (int i=0; i;>

Output

Program: Write a program to implement comb sort in Java.

  class CombSort {  static int updatedGap(int gap)  {  // Shrink gap by Shrink factor  gap = (gap*10)/13;    if (gap < 1)  return 1;  return gap;  }    // Function to sort array elements using Comb Sort  static void combSort(int a[], int n)  {  int gap = n; /* Initialize gap size equal to the size of array */    int swapped = 1;    while (gap != 1 || swapped == 1)  {  gap = updatedGap(gap); // find updated gap  // Initialize swapped as false so that we can  // check whether swap happened or not  swapped = 0;    for (int i = 0; i < n-gap; i++) /* Compare all elements     with current gap */  {  if (a[i] > a[i+gap]) //swap a[i] with a[i+gap]  {      int temp = a[i];                    a[i] = a[i+gap];                    a[i+gap] = temp;    swapped = 1;  }  }  }  }  static void printArr(int a[], int n) /* function to print array elements */  {      for (int i=0; i;>

Output

Program: Write a program to implement comb sort in PHP.

  <?php  function updatedGap($gap)  {  // Shrink gap by Shrink factor  $gap = ($gap*10)/13;    if ($gap < 1)  return 1;  return $gap;  }    // Function to sort array elements using Comb Sort  function combSort(&$a, $n)  {  $gap = $n; /* Initialize gap size equal to the size of array */    $swapped = 1;    while ($gap != 1 || $swapped == 1)  {  $gap = updatedGap($gap); // find updated gap  // Initialize swapped as false so that we can  // check whether swap happened or not  $swapped = 0;    for ($i = 0; $i < $n-$gap; $i++) /* Compare all elements with current gap */  {  if ($a[$i] > $a[$i+$gap]) //swap a[i] with a[i+gap]  {      $temp = $a[$i];                    $a[$i] = $a[$i+$gap];                    $a[$i+$gap] = $temp;    $swapped = 1;  }  }  }  }  function printArr($a, $n) /* function to print array elements */  {      for($i = 0; $i < $n; $i++)       {            print_r($a[$i]);            echo ” “;        }        }        $a = array(44, 40, 14, 43, 28, 26, 1, 5, 9);  $n = count($a);      echo “Before sorting array elements are – <br>”;        printArr($a, $n);  combSort($a,$n);      echo “<br> After sorting array elements are – <br>”;        printArr($a, $n);  ?>  

Output

So, that’s all about the article. Hope the article will be helpful and informative to you.

This article was not only limited to the algorithm. Along with the algorithm, we have also discussed the Comb Sort’s complexity, working, and implementation in different programming languages.

Next TopicCounting Sort

Comb Sort

Comb Sort Algorithm

Algorithm

Working of comb Sort Algorithm

First iteration

Second iteration

Third iteration

Fourth iteration

Fifth iteration

Comb sort complexity

1. Time Complexity

2. Space Complexity

Implementation of Comb sort

DS Array representation of Queue

DS | Array vs linked list

You may also like