69

Complement of Graph in Discrete mathematics

In discrete mathematics, the simple graph is indicated as G, and the Complement of this graph is indicated as G`. If G` is the complement of a simple graph G, then it must contain the following things:

• The complement graph must contain all the vertices of graph G.
• If there are two vertices v and w and the original graph G does not contain any edge between these vertices, in this case, the complement graph must contain an edge between these two vertices v and w.

The simple example of complement of the graph is described as follows:

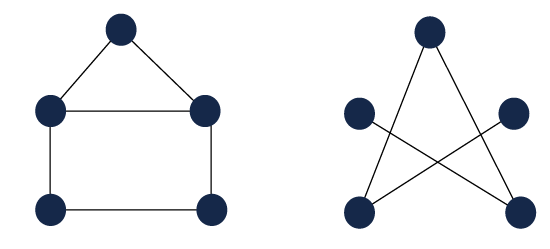
In this example, we have a simple graph on the left side, which is described as G and its complement graph on the right side, which is described as G`.

Relation between G and G`:

A simple graph G and complement graph G` contains some relations, which are described as follows:

1. The number of vertices in graph G equals to the number of vertices in its complement graph G1`. The symbolic representation of this relation is described as follows:

2. The sum of total number of edges in both the graphs, i.e., simple graph G and its complement graph G` will equal to the total number of edges in a complete graph. The symbolic representation of this relation is described as follows:

Here n is used to indicate the total number of vertices in the graph

Important Points:

When we are learning the term complement of a graph, then we should know some points, which are described as follows:

1. Size of the graph will be equal to the total number of vertices in the graph
2. Same as the Order of graph will be equal to the number of vertices in the graph

Examples of Complement of Graph

There are various examples of Complement graphs, and some of them are described as follows:

Example 1: In this example, we have a simple graph G, which contains 21 edges and 10 vertices. Now we will find out the number of edges in the graph G`.

Solution: From the question, we have the following details about graph G:

Number of vertices n = 10

Number of edges |E(G)| = 21

As we know that |E(G)| + |E(G`)| = n(n-1) /2

Now we will put the values of n and |E(G)| in this formula, and get the following details:

21 + |E(G`)| = 10*(10-1) /2

| E(G`)| = 45-21

|E(G`)| = 24

Example 2: In this example, we have a simple graph G and a complement graph G`. The graph G contains the 30 edges and G` contains the 36 edges. Now we will find out the number of vertices in graph G.

Solution: From the question, we have the following:

In graph G, the number of edges |E(G)| = 30

In graph G`, the number of edges |E(G`)| = 36

As we know that |E(G)| + |E(G`)| = n(n-1) /2

Now we will put the values of |E(G)| and |E(G`)| in this formula, and get the following details:

30+36 = n(n-1) /2

n(n-1) = 132

n² – n – 132 = 0

Now we will solve the above equation with the help of a quadratic equation. The quadratic equation is described as follows:

n = (-b ± √b² – 4ac) / 2a

When the equation is in standard form, then we will find the value of a, b and c from the original equation n² – n – 272 = 0, and plus them into the above explained quadratic formula like this:

n² – n – 132 = 0

a = 1

b = -1

c = -132

n = {-(-1) ± √(-1)² – 4*1*(-132))} / 2*1

n = {1 ± √1 – (-528)} /2

n = {1 ± 23)} /2

n = 24 /2

n = 12

Thus, graph G contains the number of vertices as G = 12.

Example 3: In this example, we have a simple graph G, which contains the order n. Here the size of a simple graph G is 56, and the size of its complement graph G` is 80. Now we will find out the value of n.

Solution: Here Size of a graph = Number of edges in graph

From the question, we have the following:

In graph G, the number of edges |E(G)| = 56

In graph G`, the number of edges |E(G`)| = 80

As we know that |E(G)| + |E(G`)| = n(n-1) /2

Now we will put the values of |E(G)| and |E(G`)|, and get the following details:

56+80 = n(n-1) /2

n(n-1) = 272

n² – n – 272 = 0

Now we will solve this equation with the help of a quadratic equation. The quadratic equation is described as follows:

n = (-b ± √b² – 4ac) / 2a

When the equation is in standard form, then we will find the value of a, b and c from the original equation n² – n – 272 = 0, and plus them into the above explained quadratic formula like this:

n² – n – 272 = 0

a = 1

b = -1

c = -272

n = {-(-1) ± √(-1)² – 4*1*(-272))} / 2*1

n = {1 ± √1 + 1088)} /2

n = {1 ± 33}

n = 34 /2

n = 17

Thus, graph G contains the number of vertices as G = 17.

In other words, we can say that the Order of graph G = 17.

---