78

Three Dimensional Transformations

The geometric transformations play a vital role in generating images of three Dimensional objects with the help of these transformations. The location of objects relative to others can be easily expressed. Sometimes viewpoint changes rapidly, or sometimes objects move in relation to each other. For this number of transformation can be carried out repeatedly.

Translation

It is the movement of an object from one position to another position. Translation is done using translation vectors. There are three vectors in 3D instead of two. These vectors are in x, y, and z directions. Translation in the x-direction is represented using T_x. The translation is y-direction is represented using T_y. The translation in the z- direction is represented using T_z.

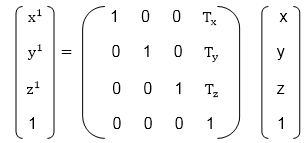
If P is a point having co-ordinates in three directions (x, y, z) is translated, then after translation its coordinates will be (x¹ y¹ z¹) after translation. T_x T_y T_z are translation vectors in x, y, and z directions respectively.

          x¹=x+ T_x
          y¹=y+T_y
          z¹=z+ T_z

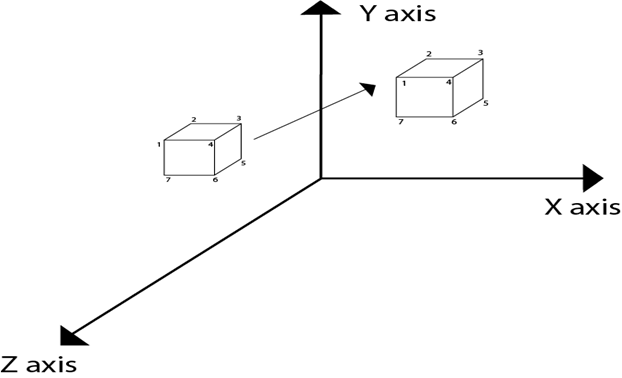
Three-dimensional transformations are performed by transforming each vertex of the object. If an object has five corners, then the translation will be accomplished by translating all five points to new locations. Following figure 1 shows the translation of point figure 2 shows the translation of the cube.

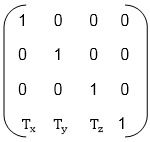
Matrix for translation

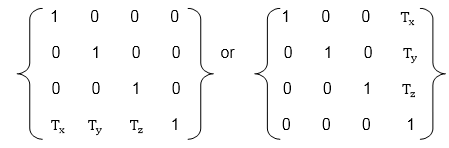
Matrix representation of point translation

Point shown in fig is (x, y, z). It become (x¹,y¹,z¹) after translation. T_x T_y T_z are translation vector.

Example: A point has coordinates in the x, y, z direction i.e., (5, 6, 7). The translation is done in the x-direction by 3 coordinate and y direction. Three coordinates and in the z- direction by two coordinates. Shift the object. Find coordinates of the new position.

Solution: Co-ordinate of the point are (5, 6, 7)
                 Translation vector in x direction = 3
                 Translation vector in y direction = 3
                 Translation vector in z direction = 2
                 Translation matrix is
                 

Multiply co-ordinates of point with translation matrix

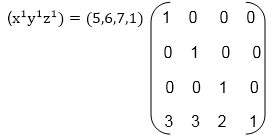
                 = [5+0+0+30+6+0+30+0+7+20+0+0+1] = [8991]

x becomes x¹=8
y becomes y¹=9
z becomes z¹=9

---