80

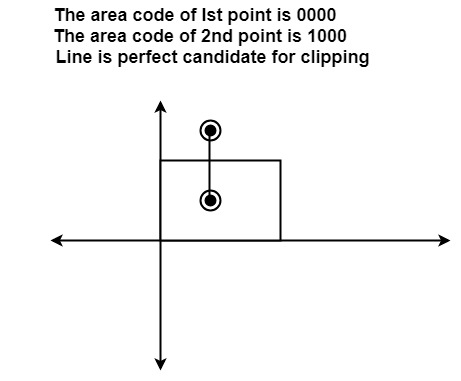
Line Clipping:

It is performed by using the line clipping algorithm. The line clipping algorithms are:

1. Cohen Sutherland Line Clipping Algorithm
2. Midpoint Subdivision Line Clipping Algorithm
3. Liang-Barsky Line Clipping Algorithm

Cohen Sutherland Line Clipping Algorithm:

In the algorithm, first of all, it is detected whether line lies inside the screen or it is outside the screen. All lines come under any one of the following categories:

1. Visible
2. Not Visible
3. Clipping Case

1. Visible: If a line lies within the window, i.e., both endpoints of the line lies within the window. A line is visible and will be displayed as it is.

2. Not Visible: If a line lies outside the window it will be invisible and rejected. Such lines will not display. If any one of the following inequalities is satisfied, then the line is considered invisible. Let A (x₁,y₂) and B (x₂,y₂) are endpoints of line.

x_min,x_max are coordinates of the window.

y_min,y_max are also coordinates of the window.
          x₁>x_max
          x₂>x_max
          y₁>y_max
          y₂>y_max
          x₁<x_min
          x₂<x_min
          y₁<y_min
          y₂<y_min

3. Clipping Case: If the line is neither visible case nor invisible case. It is considered to be clipped case. First of all, the category of a line is found based on nine regions given below. All nine regions are assigned codes. Each code is of 4 bits. If both endpoints of the line have end bits zero, then the line is considered to be visible.

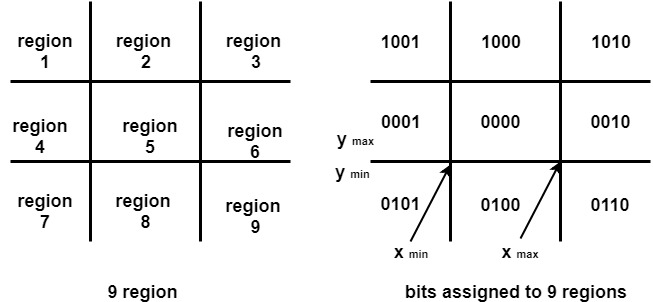
The center area is having the code, 0000, i.e., region 5 is considered a rectangle window.

Following figure show lines of various types

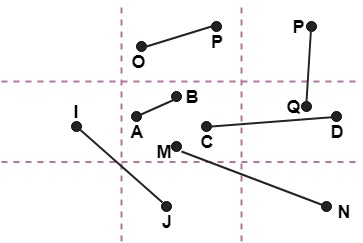
Line AB is the visible case
Line OP is an invisible case
Line PQ is an invisible line
Line IJ are clipping candidates
Line MN are clipping candidate
Line CD are clipping candidate

Advantage of Cohen Sutherland Line Clipping:

1. It calculates end-points very quickly and rejects and accepts lines quickly.
2. It can clip pictures much large than screen size.

Algorithm of Cohen Sutherland Line Clipping:

Step1:Calculate positions of both endpoints of the line

Step2:Perform OR operation on both of these end-points

Step3:If the OR operation gives 0000
       Then
                line is considered to be visible
       else
          Perform AND operation on both endpoints
      If And ≠ 0000
          then the line is invisible
        else
      And=0000
    Line is considered the clipped case.

Step4:If a line is clipped case, find an intersection with boundaries of the window
                m=(y₂-y₁ )(x₂-x₁)

(a) If bit 1 is “1” line intersects with left boundary of rectangle window
                y₃=y₁+m(x-X₁)
                where X = X_wmin
                where X_wminis the minimum value of X co-ordinate of window

(b) If bit 2 is “1” line intersect with right boundary
                y₃=y₁+m(X-X₁)
                where X = X_wmax
                where X more is maximum value of X co-ordinate of the window

(c) If bit 3 is “1” line intersects with bottom boundary
                X₃=X₁+(y-y₁)/m
                      where y = y_wmin
                y_wmin is the minimum value of Y co-ordinate of the window

(d) If bit 4 is “1” line intersects with the top boundary
                X_3=X1+(y-y₁)/m
                      where y = y_wmax
                y_wmax is the maximum value of Y co-ordinate of the window

Example of Cohen-Sutherland Line Clipping Algorithm:

Let R be the rectangular window whose lower left-hand corner is at L (-3, 1) and upper right-hand corner is at R (2, 6). Find the region codes for the endpoints in fig:

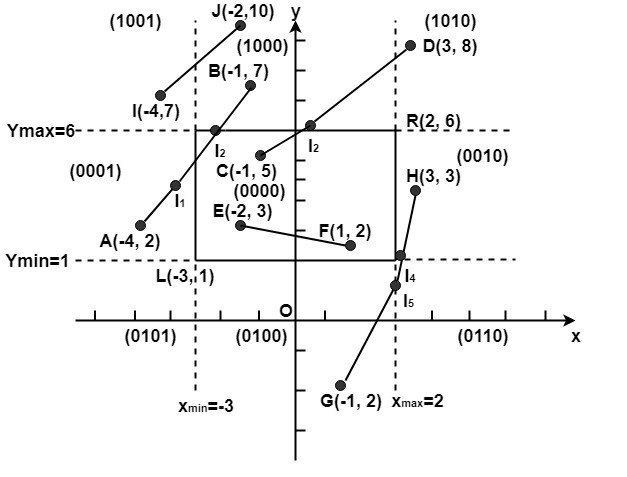
The region code for point (x, y) is set according to the scheme
Bit 1 = sign (y-y_max)=sign (y-6)         Bit 3 = sign (x-x_max)= sign (x-2)
Bit 2 = sign (y_min-y)=sign(1-y)         Bit 4 = sign (x_min-x)=sign(-3-x)

Here

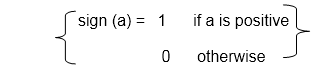
So

                A (-4, 2)→ 0001         F (1, 2)→ 0000
                B (-1, 7) → 1000         G (1, -2) →0100
                C (-1, 5)→ 0000         H (3, 3) → 0100
                D (3, 8) → 1010         I (-4, 7) → 1001
                E (-2, 3) → 0000         J (-2, 10) → 1000

We place the line segments in their appropriate categories by testing the region codes found in the problem.

Category1 (visible): EF since the region code for both endpoints is 0000.

Category2 (not visible): IJ since (1001) AND (1000) =1000 (which is not 0000).

Category 3 (candidate for clipping): AB since (0001) AND (1000) = 0000, CD since (0000) AND (1010) =0000, and GH. since (0100) AND (0010) =0000.

The candidates for clipping are AB, CD, and GH.

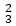
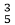
In clipping AB, the code for A is 0001. To push the 1 to 0, we clip against the boundary line x_min=-3. The resulting intersection point is I₁ (-3,3). We clip (do not display) AI₁ and I₁ B. The code for I₁is 1001. The clipping category for I₁ B is 3 since (0000) AND (1000) is (0000). Now B is outside the window (i.e., its code is 1000), so we push the 1 to a 0 by clipping against the line y_max=6. The resulting intersection is l₂ (-1,6). Thus I₂ B is clipped. The code for I₂ is 0000. The remaining segment I₁ I₂ is displayed since both endpoints lie in the window (i.e., their codes are 0000).

For clipping CD, we start with D since it is outside the window. Its code is 1010. We push the first 1 to a 0 by clipping against the line y_max=6. The resulting intersection I₃ is (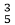,6),and its code is 0000. Thus I₃ D is clipped and the remaining segment CI₃ has both endpoints coded 0000 and so it is displayed.

For clipping GH, we can start with either G or H since both are outside the window. The code for G is 0100, and we push the 1 to a 0 by clipping against the line y_min=1.The resulting intersection point is I₄ (2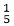,1) and its code is 0010. We clip GI₄ and work on I₄ H. Segment I₄ H is not displaying since (0010) AND (0010) =0010.

Program to perform Line Clipping using Cohen Sutherland Algorithm:

Output:

---