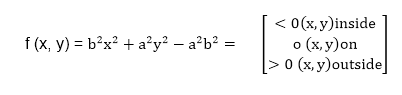Midpoint Ellipse Algorithm:

This is an incremental method for scan converting an ellipse that is centered at the origin in standard position i.e., with the major and minor axis parallel to coordinate system axis. It is very similar to the midpoint circle algorithm. Because of the four-way symmetry property we need to consider the entire elliptical curve in the first quadrant.

Let’s first rewrite the ellipse equation and define the function f that can be used to decide if the midpoint between two candidate pixels is inside or outside the ellipse:

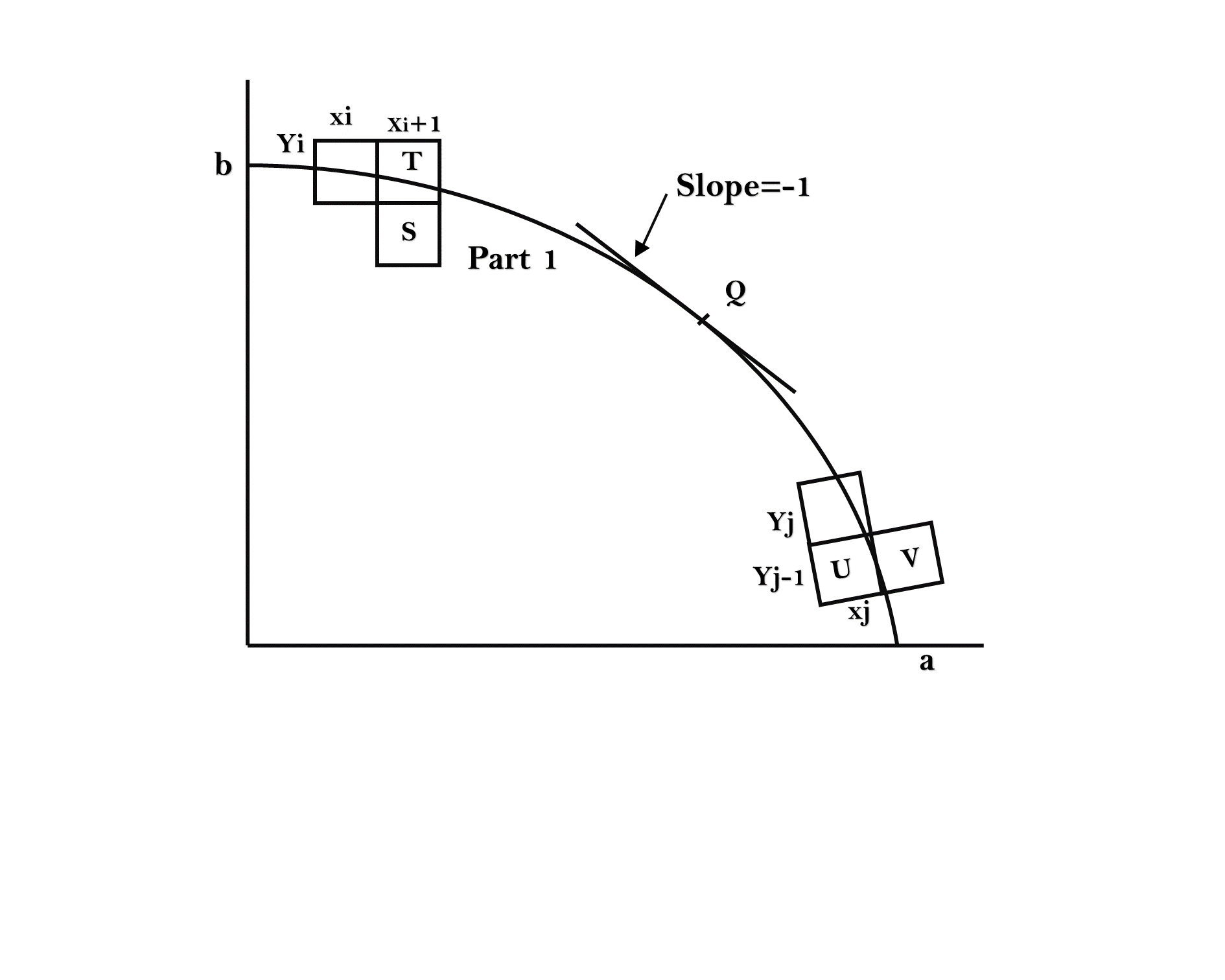
Now divide the elliptical curve from (0, b) to (a, 0) into two parts at point Q where the slope of the curve is -1.

Slope of the curve is defined by the f(x, y) = 0 is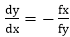where fx & fy are partial derivatives of f(x, y) with respect to x & y.

We have fx = 2b² x, fy=2a² y & 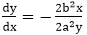Hence we can monitor the slope value during the scan conversion process to detect Q. Our starting point is (0, b)

Suppose that the coordinates of the last scan converted pixel upon entering step i are (x_i,y_i). We are to select either T (x_i+1),y_i) or S (x_i+1,y_i-1) to be the next pixel. The midpoint of T & S is used to define the following decision parameter.

pi = f(x_i+1),y_i–)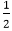
pi=b² (x_i+1)²+a² (y_i–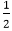)²-a² b²

If pi<0, the midpoint is inside the curve and we choose pixel T.

If pi>0, the midpoint is outside or on the curve and we choose pixel S.

Decision parameter for the next step is:

p_i+1=f(x_i+1+1,y_i+1–)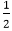
          = b² (x_i+1+1)²+a² (y_i+1–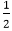)²-a² b²

Since x_i+1=xi+1,we have
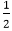
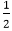
          p_i+1-pi=b²[((x_i+1+1)²+a² (y_i+1–)²-(y_i –)²]
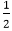
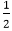
          p_i+1= pi+2b² x_i+1+b²+a² [(y_i+1–)²-(y_i –)²]

If T is chosen pixel (pi<0), we have y_i+1=yi.

If S is chosen pixel (pi>0) we have y_i+1=yi-1. Thus we can express

          p_i+1in terms of pi and (x_i+1,y_i+1):           p_i+1= pi+2b² x_i+1+b²          if pi<0           = pi+2b² x_i+1+b²-2a² y_i+1 if pi>0

The initial value for the recursive expression can be obtained by the evaluating the original definition of pi with (0, b):

p1 = (b²+a² (b-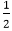)²-a² b²
= b²-a² b+a²/4

Suppose the pixel (x_j y_j) has just been scan converted upon entering step j. The next pixel is either U (x_j ,y_j-1) or V (x_j+1,y_j-1). The midpoint of the horizontal line connecting U & V is used to define the decision parameter:

q_j=f(x_j+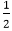,y_j-1)
q_j=b² (x_j+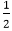)²+a² (y_j -1)²-a² b²

If q_j<0, the midpoint is inside the curve and we choose pixel V.

If q_j≥0, the midpoint is outside the curve and we choose pixel U.Decision parameter for the next step is:

q_j+1=f(x_j+1+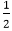,y_j+1-1)
          = b² (x_j+1+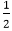)²+ a² (y_j+1-1)²– a² b²

Since y_j+1=y_j-1,we have
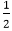
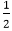
q_j+1-q_j=b² [(x_j+1+)²-(x_j +)² ]+a² (y_j+1-1)²-( y_j+1)² ]
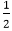
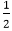
q_j+1=q_j+b² [(x_j+1+)²-(x_j +)²]-2a² y_j+1+a²

If V is chosen pixel (qj<0), we have x_j+1=xj.

If U is chosen pixel (pi>0) we have x_j+1=xj. Thus we can express

q_j+1in terms of q_j and (x_j+1,y_j+1 ):
q_j+1=q_j+2b² x_j+1-2a² y_j+1+a²          if qj < 0
=q_j-2a² y_j+1+a²          if qj>0

The initial value for the recursive expression is computed using the original definition of qj. And the coordinates of (x_k y_k) of the last pixel choosen for the part 1 of the curve:

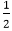
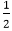
q1 = f(x_k+,y_k-1)=b² (x_k+)²-a² (y_k-1)²– a² b²

Algorithm:

int x=0, y=b; [starting point]  int fx=0, fy=2a2 b [initial partial derivatives]  int p = b2-a2 b+a2/4  while (fx2;  if (p<0)  p = p + fx +b2;  else  {  y--;  fy=fy-2a2  p = p + fx +b2-fy;  }  }  Setpixel (x, y);  p=b2(x+0.5)2+ a2 (y-1)2- a2 b2  while (y>0)  {  y--;  fy=fy-2a2;  if (p>=0)  p=p-fy+a2             else  {  x++;  fx=fx+2b2  p=p+fx-fy+a2;  }  Setpixel (x,y);  }  )>

Program to draw an ellipse using Midpoint Ellipse Algorithm:

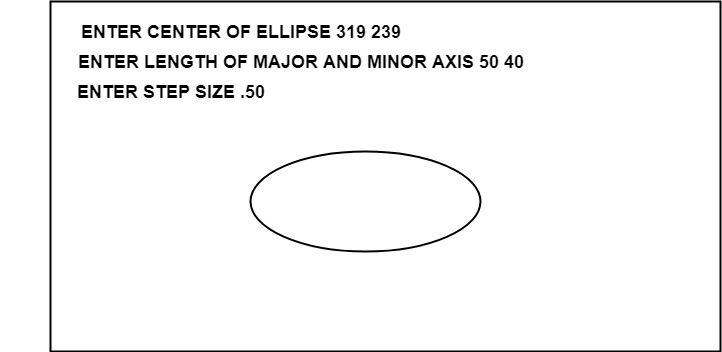
Output: