Computer Graphics Polynomial Method

by Online Tutorials Library July 14, 2022

Polynomial Method:

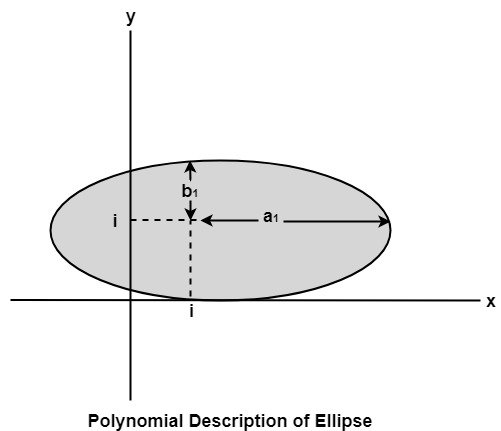
The ellipse has a major and minor axis. If a₁ and b₁are major and minor axis respectively. The centre of ellipse is (i, j). The value of x will be incremented from i to a₁and value of y will be calculated using the following formula

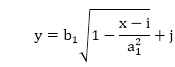
Drawback of Polynomial Method:

It requires squaring of values. So floating point calculation is required.
Routines developed for such calculations are very complex and slow.

Algorithm:

1. Set the initial variables: a = length of major axis; b = length of minor axis; (h, k) = coordinates of ellipse center; x = 0; i = step; x_end = a.

2. Test to determine whether the entire ellipse has been scan-converted. If x>x_end, stop.

3. Compute the value of the y coordinate:

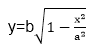
4. Plot the four points, found by symmetry, at the current (x, y) coordinates:

Plot (x + h, y + k) Plot (-x + h, -y + k) Plot (-y – h, x + k) Plot (y + h, -x + k)

5. Increment x; x = x + i.

6. Go to step 2.

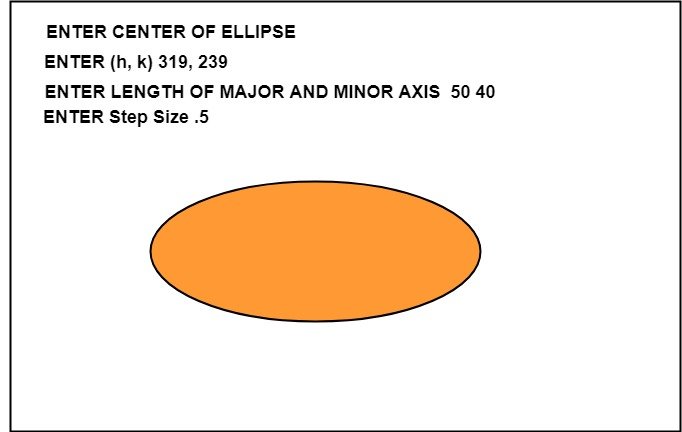
Program to draw an Ellipse using Polynomial Method:

  #include   #include   #include   #include   #include   #include     class bresen  {  float x, y, a, b, r, t, te, xend, h, k, step;  public:  void get ();  void cal ();  };  void main ()      {  bresen b;  b.get ();  b.cal ();  getch ();     }  void bresen :: get ()     {  cout<<“n ENTER CENTER OF ELLIPSE”;  cout<<“n enter (h, k) “;  cin>>h>>k;  cout<<“n ENTER LENGTH OF MAJOR AND MINOR AXIS”;  cin>>a>>b;  cout<<“n ENTER Step Size”;  cin>> step;     }  void bresen ::cal ()  {  /* request auto detection */  int gdriver = DETECT,gmode, errorcode;  int midx, midy, i;  /* initialize graphics and local variables */  initgraph (&gdriver, &gmode, ” “);  /* read result of initialization */  errorcode = graphresult ();  if (errorcode ! = grOK)    /*an error occurred */  {   printf(“Graphics error: %s n”, grapherrormsg (errorcode);  printf (“Press any key to halt:”);  getch ();  exit (1); /* terminate with an error code */  }  x = 0;  xend=a;  whilex (x)>

Output:

Next TopicTrignometric Method

2d transformation 3d computer graphics 3d transformation animation techniques cathode ray tube circle generation algorithm color crt monitors computer animation computer graphics tutorial crt curves display processor flat panel display fractals introduction keyframing line generation algorithm polygon filling algorithm random scan display raster scan display surfaces types of curves viewing and clipping

Computer Graphics Polynomial Method

Polynomial Method:

Drawback of Polynomial Method:

Algorithm:

Program to draw an Ellipse using Polynomial Method:

Why is my Internet connection so slow

BGP | Border Gateway Protocol

You may also like