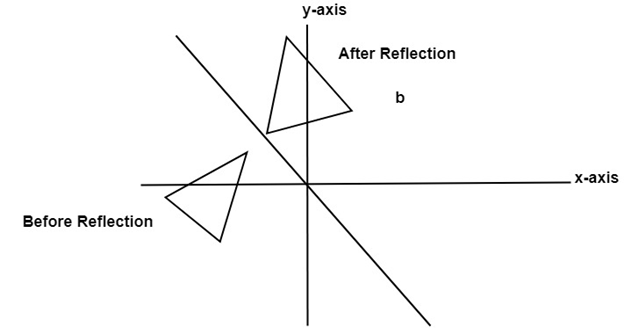
Reflection:

It is a transformation which produces a mirror image of an object. The mirror image can be either about x-axis or y-axis. The object is rotated by180°.

Types of Reflection:

Reflection about the x-axis
Reflection about the y-axis
Reflection about an axis perpendicular to xy plane and passing through the origin
Reflection about line y=x

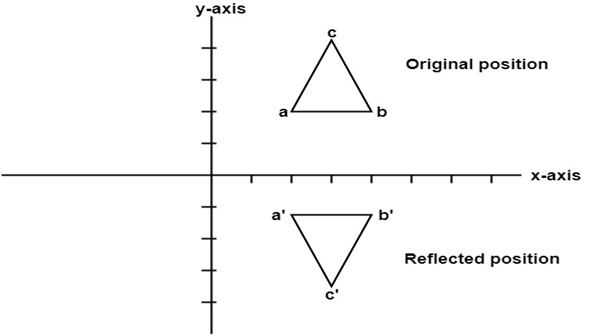
1. Reflection about x-axis: The object can be reflected about x-axis with the help of the following matrix

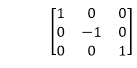
In this transformation value of x will remain same whereas the value of y will become negative. Following figures shows the reflection of the object axis. The object will lie another side of the x-axis.

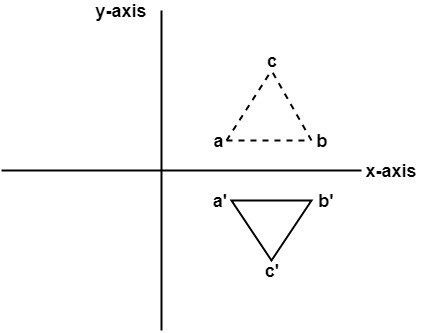
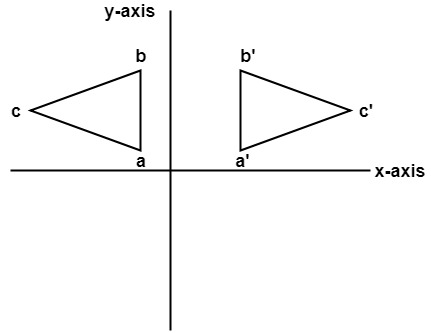
2. Reflection about y-axis: The object can be reflected about y-axis with the help of following transformation matrix

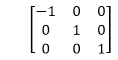
Here the values of x will be reversed, whereas the value of y will remain the same. The object will lie another side of the y-axis.

The following figure shows the reflection about the y-axis

3. Reflection about an axis perpendicular to xy plane and passing through origin:
In the matrix of this transformation is given below

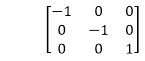
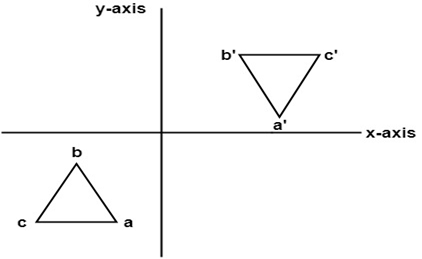
In this value of x and y both will be reversed. This is also called as half revolution about the origin.

4. Reflection about line y=x: The object may be reflected about line y = x with the help of following transformation matrix

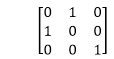
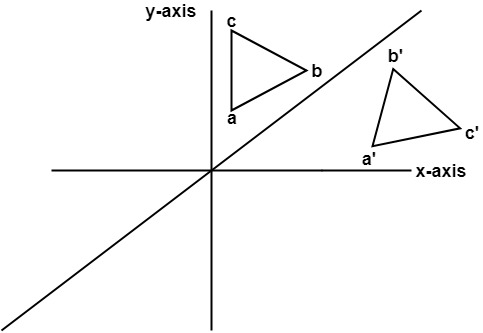
First of all, the object is rotated at 45°. The direction of rotation is clockwise. After it reflection is done concerning x-axis. The last step is the rotation of y=x back to its original position that is counterclockwise at 45°.

Example: A triangle ABC is given. The coordinates of A, B, C are given as

A (3 4)
B (6 4)
C (4 8)

Find reflected position of triangle i.e., to the x-axis.

Solution:

The a point coordinates after reflection

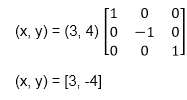
The b point coordinates after reflection

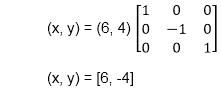
The coordinate of point c after reflection

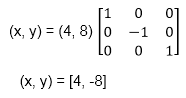
a (3, 4) becomes a¹ (3, -4)
b (6, 4) becomes b¹ (6, -4)
c (4, 8) becomes c¹ (4, -8)

Program to perform Mirror Reflection about a line:

  #include <iostream.h>  #include <conio.h>  #include <graphics.h>  #include <math.h>  #include <stdlib.h>  #define pi 3.14  class arc  {  float x[10],y[10],theta,ref[10][10],ang;             float p[10][10],p1[10][10],x1[10],y1[10],xm,ym;  int i,k,j,n;  public:  void get();  void cal ();  void map ();  void graph ();  void plot ();  void plot1();  };  void arc::get ()  {  cout<<“n ENTER ANGLE OF LINE INCLINATION AND Y INTERCEPT”;  cin>> ang >> b;  cout <<“n ENTER NO OF VERTICES”;  cin >> n;  cout <<“n ENTER”;  for (i=0; i<n; i++)  {  cout<<“n x[“<<i<<“] and y[“<<i<<“]”;  }  theta =(ang * pi)/ 180;  ref [0] [0] = cos (2 * theta);  ref [0] [1] = sin (2 * theta);  ref [0] [2] = -b *sin (2 * theta);  ref [1] [0] = sin (2 * theta);  ref [1] [1] = -cos (2 * theta);  ref [1] [2] = b * (cos (2 * theta)+1);  ref [2] [0]=0;  ref [2] [1]=0;  ref [2] [2] = 1;  }  void arc :: cal ()  {  for (i=0; i < n; i++)  {  p[0] [i] = x [i];  p [1] [i] = y [i];  p [2] [i] = 1;  }  for (i=0; i<3;i++)  {  for (j=0; j<n; j++)  {  p1 [i] [j]=0;  for (k=0;k<3; k++)  }  p1 [i] [j] + = ref [i] [k] * p [k] [j];               }  for (i=0; i<n; i++)     {  x1 [i]=p1[0] [i];  y1 [i] = p1 [1] [i];      }  }  void arc :: map ()  {  int gd = DETECT,gm;  initgraph (&gd, &gm, ” “);              int errorcode = graphresult ();  /* an error occurred */  if (errorcode ! = grOK)      {   printf (“Graphics error: %s n”, grapherrormsg (errorcode));  printf (“Press any key to halt:”);  getch ();  exit (1); /* terminate with an error code */  }  }  void arc :: graph ()  {  xm=getmaxx ()/2;  ym=getmaxy ()/2;  line (xm, 0, xmm 2*ym);  }  void arc :: plot 1 ()  {  for (i=0; i <n-1; i++)  {  circle (x1[i]+xm, (-y1[i]+ym), 2);  line (x1[i]+xm, (-y1[i]+ym), x1[i+1]+xm, (-y1[i+1]+ym));  }  line (x1[n-1)+xm, (-y1[n-1]+ym), x1[0]+xm, (-y1[0]+ym));  getch();  }  void arc :: plot ()  {   for (i=0; i <n-1; i++)  {  circle (x1[i]+xm, (-y1[i]+ym, 2);  line (x1[i]+xm, (-y1[i]+ym), x[i+1]+xm, (-y1[i+1]+ym));  }  line (x[n-1]+xm, (-y1[n-1]+ym), x[0]+xm, (-y[0]+ym));  getch();  }  void main ()  {  class arc a;  clrscr();  a.map();  a.graph();  a.get();  a.cal();  a.plot();  a.plot1();  getch();  }  

Output:

Next TopicShearing

2d transformation 3d computer graphics 3d transformation animation techniques cathode ray tube circle generation algorithm color crt monitors computer animation computer graphics tutorial crt curves display processor flat panel display fractals introduction keyframing line generation algorithm polygon filling algorithm random scan display raster scan display surfaces types of curves viewing and clipping

Computer Graphics Reflection

Reflection:

Types of Reflection:

Program to perform Mirror Reflection about a line:

Why is my Internet connection so slow

BGP | Border Gateway Protocol

You may also like