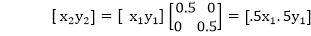Scaling:
It is used to alter or change the size of objects. The change is done using scaling factors. There are two scaling factors, i.e. Sx in x direction Sy in y-direction. If the original position is x and y. Scaling factors are Sx and Sy then the value of coordinates after scaling will be x1 and y1.
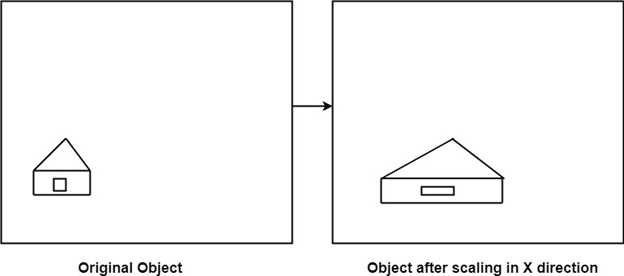
If the picture to be enlarged to twice its original size then Sx = Sy =2. If Sxand Sy are not equal then scaling will occur but it will elongate or distort the picture.
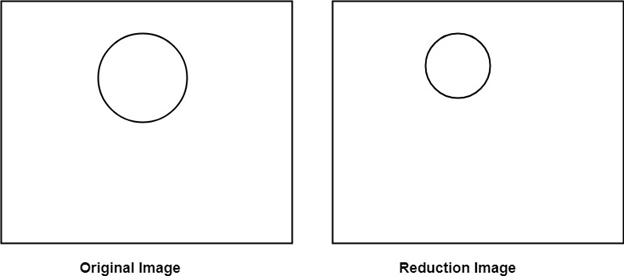
If scaling factors are less than one, then the size of the object will be reduced. If scaling factors are higher than one, then the size of the object will be enlarged.
If Sxand Syare equal it is also called as Uniform Scaling. If not equal then called as Differential Scaling. If scaling factors with values less than one will move the object closer to coordinate origin, while a value higher than one will move coordinate position farther from origin.
Enlargement: If T1=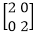
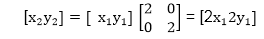
,If (x1 y1)is original position and T1is translation vector then (x2 y2) are coordinated after scaling
The image will be enlarged two times
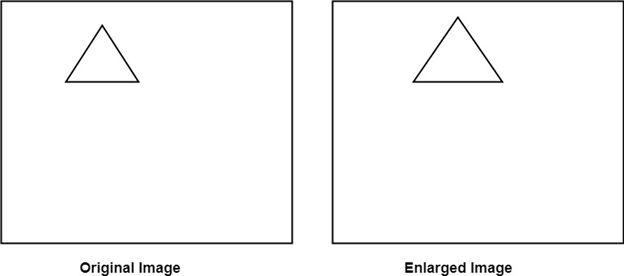
Reduction: If T1=
. If (x1 y1) is original position and T1 is translation vector, then (x2 y2) are coordinates after scaling
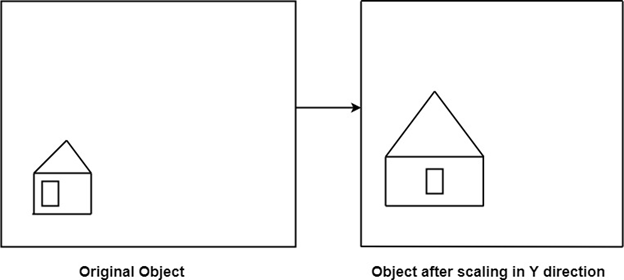
Matrix for Scaling:
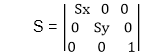
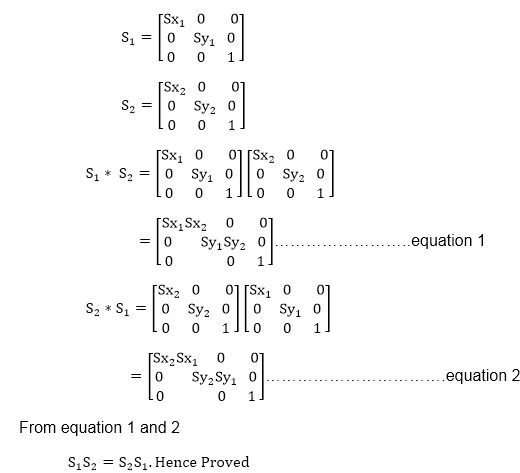
Example: Prove that 2D Scaling transformations are commutative i.e, S1 S2=S2 S1.
Solution: S1 and S2 are scaling matrices
