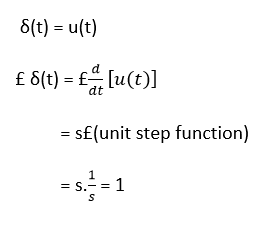Transient and Steady State Analysis of Linear Time Invariant (LTI) Systems
Time Response Analysis
When the energy state of any system is disturbed, and the disturbances occur at input, output or both ends, then it takes some time to change from one state to another state. This time that is required to change from one state to another state is known as transient time and the value of current and voltage during this period is called transient response.
Depending upon the parameters of the system, the transient may have oscillations which may be either sustained or decaying in nature.
Thus time response of a control system is divided into two parts-
- Transient response analysis.
- Steady State Analysis.
Transient State response
It deals with the nature of the response of a system when subjected to an input.
Steady State Analysis
It deals with the estimation of the magnitude of steady-state error between input and output.
Different Type of Standard Test Signals
The various inputs or disturbances affecting the performance of a system are mathematically represented as a standard test signal.
- Step signal ( sudden input )
- Ramp Signal (velocity type of input )
- Parabolic Signal ( type of acceleration input )
- Impulse signal (sudden shock )
NOTE
- Step signal and impulse signal are bounded input signal.
- Ramp signal and parabolic signal are an unbounded input signal.
- Step signal, a ramp signal, and periodic signal are for time domain analysis. Only an impulse signal is essential for steady-state analysis.
Characteristics of Time-domain Analysis
- Every transfer function representing the control system is of a particular type of order.
- The steady state analysis depends upon the type of the system.
- The type of the system is determined from open loop transfer function G(S).H(S)
Transient Time: The time required to change from one state to another is called the transient time.
Transient Response: The value of current and voltage during the time change is called transient response.
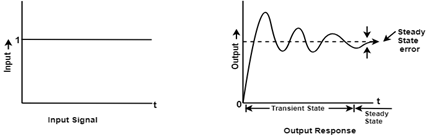
So, we can say that the transient response is the part of the response which goes to zero as time increases and the steady-state response is the part of the total response after transient has died. If the steady-state response is the part of the output does not match with the input then the system has a steady state error.
Test input signal for transient analysis
For the analysis of the time response of a control system, the following input signals are used.
Step Function
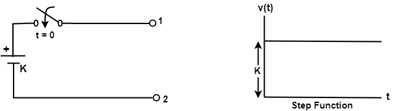
A unit step function is denoted by u(t) and is defined as
Laplace Transform:
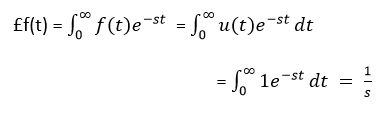
Step function is also called displacement function. If input is R(S), then R(s) = 1/s
Ramp Function
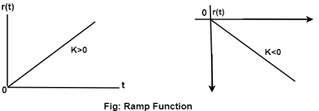
This function starts from the origin and linearly decreases or increases with time as shown in the figure above.
Let r(t) be the ramp function then
Where ‘K’ is the slope of the line, for a positive value of ‘K’ the slope is upward, and the slope is downward for the negative value of ‘K.’
Laplace transform
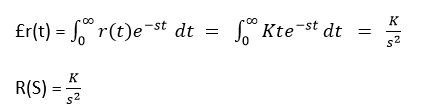
Parabolic Function
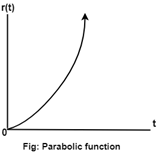
The value of r(t) is zero when t<0 and is a quadratic function of time when t>0.
Where ‘K’ is constant for unit parabolic function K = 1. The unit parabolic function is defined as
Laplace Transform
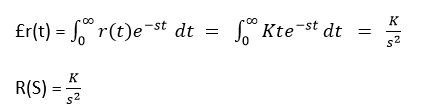
Impulse Function
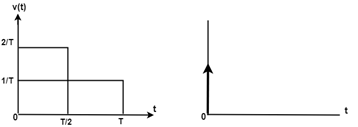
A unit impulse function is defined as
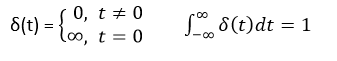
Thus we can say that impulse function has zero value everywhere except at t=0 where the amplitude is infinite.