BCD to Excess-3 conversion
To understand the process of converting BCD to Excess-3, it is required to have knowledge of Number System and Number Base Conversion.
The Excess-3 binary code is an example of a self-complementary BCD code. A self-complementary binary code is a code which is always complimented in itself. By replacing the bit 0 to 1 and 1 to 0 of a number, we find the 1’s complement of the number. The sum of the 1’st complement and the binary number of a decimal is equal to the binary number of decimal 9.
The process of converting BCD to Excess-3 is quite simple from other conversions. The Excess-3 code can be calculated by adding 3, i.e., 0011 to each four-digit BCD code. Below is the truth table for the conversion of BCD to Excess-3 code. In the below table, the variables A, B, C, and D represent the bits of the binary numbers. The variable ‘D’ represents the LSB, and the variable ‘A’ represents the MSB. In the same way, the variables w, x, y, and z represent the bits of the Excess-3 code. The variable ‘z’ represents the LSB, and the variable ‘w’ represents the MSB. The ‘don’t care conditions’ is expressed by the variable ‘X’.
| Decimal Number | BCD Code | Excess-3 Code | ||||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | D | W | x | y | z | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 3 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 5 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 6 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 7 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 8 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 9 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 10 | 1 | 0 | 1 | 0 | X | X | X | X |
| 11 | 1 | 0 | 1 | 1 | X | X | X | X |
| 12 | 1 | 1 | 0 | 0 | X | X | X | X |
| 13 | 1 | 1 | 0 | 1 | X | X | X | X |
| 14 | 1 | 1 | 1 | 0 | X | X | X | X |
| 15 | 1 | 1 | 1 | 1 | X | X | X | X |
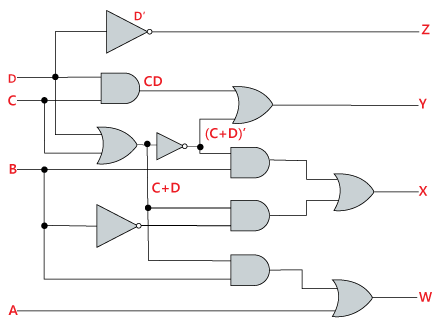
Now, we will use the K-map method to design the logical circuit for the conversion of BCD to Excess-3 code as:
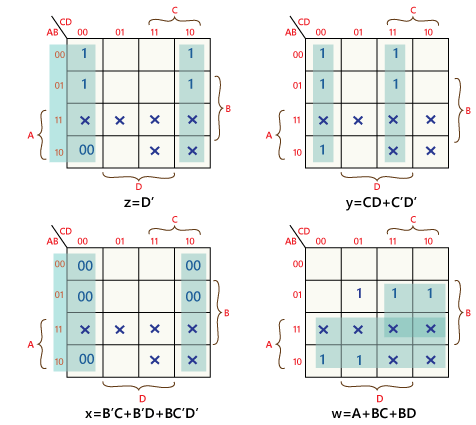
So,
w=A+BC+BD
x=B’ C+B’ D+BC’ D’
y=CD+C’D’
z=D’
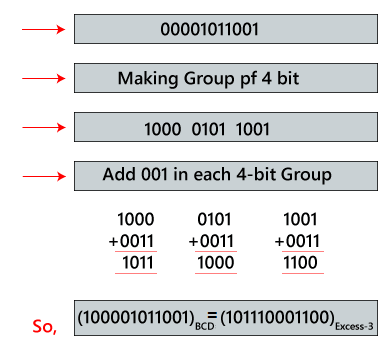
Example: (100001011001)BCD
To find the Excess-3 code of the given Excess-3 code, first, we will make the group of 4 bits from right to left. Then, we will add 0011 in each group of 4 bits in order to get the excess-3 code.
Excess-3 to BCD conversion
The process of converting Excess-3 to BCD is opposite to the process of converting BCD to Excess-3. The BCD code can be calculated by subtracting 3, i.e., 0011 from each four-digit Excess-3 code. Below is the truth table for the conversion of Excess-3 code to BCD. In the below table, the variables w, x, y, and z represent the bits of the Excess-3 code. The variable ‘z’ represents the LSB, and the variable ‘w’ represents the MSB. In the same way, the variables A, B, C, and D represent the bits of the binary numbers. The variable ‘D’ represents the LSB, and the variable ‘A’ represents the MSB. The ‘don’t care conditions’ is defined by the variable ‘X’.
| Decimal Number | Excess-3 Code | BCD Code | ||||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | D | W | x | y | z | |
| 0 | 0 | 0 | 0 | 0 | X | X | X | X |
| 1 | 0 | 0 | 0 | 1 | X | X | X | X |
| 2 | 0 | 0 | 1 | 0 | X | X | X | X |
| 3 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 5 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 7 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 8 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 10 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 11 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 12 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 13 | 1 | 1 | 0 | 1 | X | X | X | X |
| 14 | 1 | 1 | 1 | 0 | X | X | X | X |
| 15 | 1 | 1 | 1 | 1 | X | X | X | X |
Now, we will use the K-map method to design the logical circuit for the conversion of Excess-3 code to BCD as:
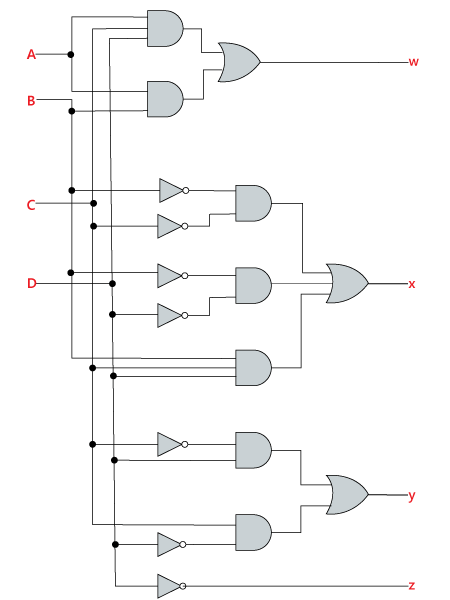
So,
w=AB+ACD
B=x’ y’+x’ z’+xyz
C=y’ z+yz’
D=z’
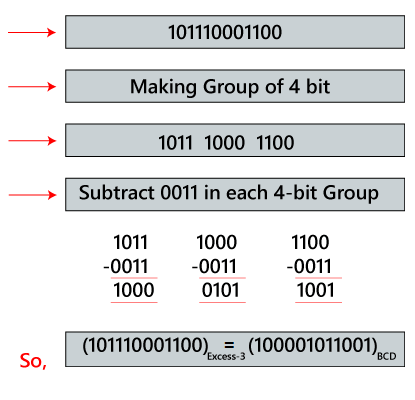
Example: (101110001100)Excess-3
To find the BCD code of the given BCD number, first, we make the group of 4 bits from right to left. Then, we subtract 0011 in each group of 4 bits in order to get the BCD code.