C++ Dijkstra Algorithm using the priority queue

In this article, we will see the implementation of the Dijkstra algorithm using the priority queue of C++ STL. Dijkstra algorithm is used to find the shortest path from the source to the destination in an undirected graph.

A graph having weight on the edges is given as below:

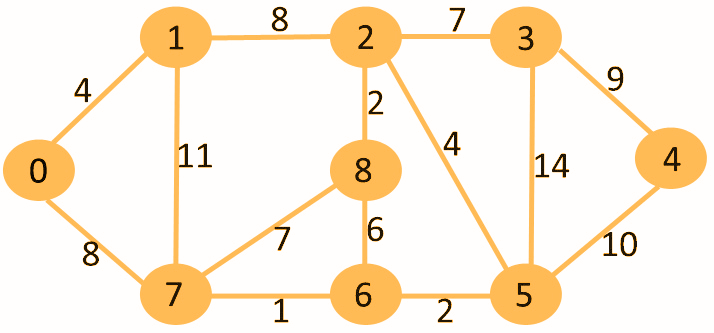
Let us consider a source vertex 0, we have to find the shortest path from the source vertex to all the vertices in the graph.

Source vertex = 0

Vertex	Distance from source
0	0 Same source and destination
1	4 Directly goes to 1
2	12 Path: 0 ->1 -> 2 (8 + 4 = 12)
3	19 Path: 0 ->1 -> 2 -> 3 (8 + 4 + 7 = 19)
4	21 Path: 0 -> 7 -> 6 -> 5 -> 4 (8 + 1 + 2 + 10 = 21)
5	11 Path: 0 -> 7 -> 6 -> 5 (8 + 1 + 2 = 11)
6	9 Path: 0 -> 7 -> 6 (8 + 1 = 9)
7	8 Path: 0 -> 7
8	14 Path: 0 -> 1 -> 2 -> 8 (4 + 8 + 2 = 14)

Create graph structure

We will create a class Graph with data members as

int v – To store the number of vertices in the graph
List of pairs – To store the vertex and the weight associated with a particular vertex.

list> *adj;,pair>

Constructors:

We need a constructor to allocate the memory of the adjacency list.

  Graph(int vertex)  {  this->V = vertex; // Allocate the number of vertices   adj = list [vertex]; // Allocate memory for adjacency list   }  

How to add an edge to the graph?

The list of pairs created has two arguments. One will contain the vertex, and the other will contain the weight associated with it.

As the graph is bidirectional, we can add the same weight to the opposite vertex.

Code:

   void addanEdge(int u, int v, int w)  {  adj[u].push_back(make_pair(v,w)); // add v to w   adj[v].push_back(make_pair(u,w)); add w to v   // To add a vertex with weight associated with it   }  

Algorithm

Mark initial distance from the source is infinite.
Create an empty priority_queue PQ. Every item of PQ is a pair (weight, vertex). Weight (or distance) is used as the first item of pair as the first item is by default used to compare two pairs.
Insert source vertex into PQ and make its distance as 0.
Until the priority queue defined as PQ does not become empty. Perform the operations a and b.
1. Extract minimum distance vertex from PQ and let it be u.
2. Loop through all adjacent of u and do
  Following for every vertex v.
  // If there is a shorter path to v
  // through u.
  If dist[v] > dist[u] + weight(u, v) // distance of ( v) > distance of (u) and weight from u to v
  1. Update distance of v, i.e., do
    dist[v] = dist[u] + weight(u, v)
  2. Insert v into the pq (Even if v is
    already there)
Loop through the dist[] array to print the shortest paths from source to all the vertices.

C++ code

  #include   using namespace std;  #define INF 0x3f3f3f3f // The distance to other vertices is initialized as infinite  // iPair ==> Integer Pair  typedef pair iPair;  class Graph // Graph structure      {      int V; // No. of vertices in the graph      list>* adj; // the list of pair to store vertex and its weight  public:      // Constructor that accept number of vertices in graph      Graph(int V) // allocate the vertex memory      {          this->V = V; // assign the vertex           adj = new list[V]; // allocate space for vertices       }      void addEdge(int u, int v, int w); // add edges in the graph      // prints shortest path from s      void shortestPathingraph(int s); // pass source vertex  };  void Graph::addEdge(int u, int v, int w) // add an edge  {      adj[u].push_back(make_pair(v, w)); // make a pair of vertex and weight and // add it to the list      adj[v].push_back(make_pair(u, w)); // add oppositely by making a pair of weight and vertex  }  // Calling function outside the Graph class  void Graph::shortestPathingraph(int src) // src is the source vertex  {      // Create a priority queue to store vertices that      // are being preprocessed.      priority_queue, greater> pq;      vector dist(V, INF); // All distance from source are infinite      pq.push(make_pair(0, src)); // push spurce node into the queue      dist[src] = 0; // distance of source will be always 0      while (!pq.empty()) { // While queue is not empty          // Extract the first minimum distance from the priority queue          // vertex label is stored in second of pair (it          // has to be done this way to keep the vertices          // sorted distance          int u = pq.top().second;          pq.pop();          // ‘i’ is used to get all adjacent vertices of a vertex          list>::iterator i;          for (i = adj[u].begin(); i != adj[u].end(); ++i) {              // Get vertex label and weight of current adjacent              // of u.              int v = (*i).first;              int weight = (*i).second;                // If there is shorted path to v through u.              if (dist[v] > dist[u] + weight) {                  // Updating distance of v                  dist[v] = dist[u] + weight;                  pq.push(make_pair(dist[v], v));              }          }      }      printf(“Vertex tDistance from Sourcen”); // Print the result      for (int i = 0; i < V; ++i)          printf(“%d tt %dn”, i, dist[i]); // The shortest distance from source  }  int main()  {      int V = 9; // vertices in given graph are 9      Graph g(V); //  call Constructor by creating an object of graph      g.addEdge(0, 1, 4); // add root node with neighour vertex and weight      g.addEdge(0, 7, 8);      g.addEdge(1, 2, 8);      g.addEdge(1, 7, 11);      g.addEdge(2, 3, 7);      g.addEdge(2, 8, 2);      g.addEdge(2, 5, 4);      g.addEdge(3, 4, 9);      g.addEdge(3, 5, 14);      g.addEdge(4, 5, 10);      g.addEdge(5, 6, 2);      g.addEdge(6, 7, 1);      g.addEdge(6, 8, 6);      g.addEdge(7, 8, 7);      g.shortestPathingraph(0); // call the function to find shortest path of graph      return 0; // end of main function()  }  ,>,>

Output

Vertex   Distance from Source  0    0  1    4  2   12  3   19  4   21  5   11  6    9  7            8  8   14

Next TopicConstructor overloading in C++

C++ Dijkstra Algorithm using the priority queue

C++ Dijkstra Algorithm using the priority queue

Create graph structure

How to add an edge to the graph?

Algorithm

C++ code

Array of sets in C++

C++ Program to Convert Number in Character

You may also like