The Empirical Rule, sometimes called the 68-95-99.7 rule, states that for a given dataset with a normal distribution:
- 68% of data values fall within one standard deviation of the mean.
- 95% of data values fall within two standard deviations of the mean.
- 99.7% of data values fall within three standard deviations of the mean.
In this tutorial, we explain how to apply the Empirical Rule in Excel to a given dataset.
Applying the Empirical Rule in Excel
Suppose we have a normally-distributed dataset with a mean of 7 and a standard deviation of 2.2. The following screenshot shows how to apply the Empirical Rule to this dataset in Excel to find which values 68% of the data falls between, which values 95% of the data falls between, and which values 99.7% of the data falls between:
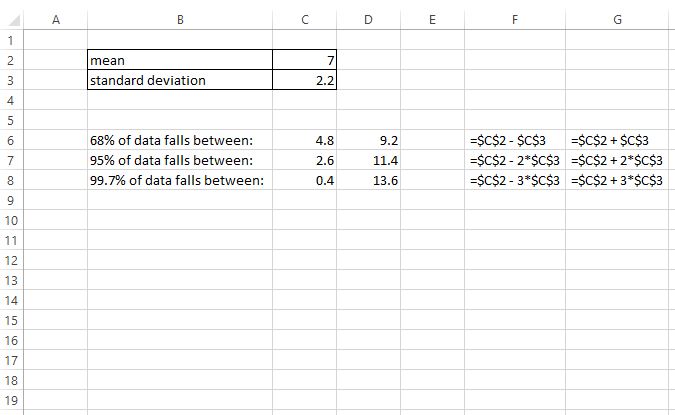
From this output, we can see:
- 68% of the data falls between 4.8 and 9.2
- 95% of the data falls between 2.6 and 11.4
- 99.7% of the data falls between 0.4 and 13.6
The cells in columns F and G show the formulas that were used to find these values.
To apply the Empirical Rule to a different dataset, we simply need to change the mean and standard deviation in cells C2 and C3. For example, here is how to apply the Empirical Rule to a dataset with a mean of 40 and a standard deviation of 3.75:

From this output, we can see:
- 68% of the data falls between 36.25 and 43.75
- 95% of the data falls between 32.5 and 47.5
- 99.7% of the data falls between 28.75 and 51.25
And here is one more example of how to apply the Empirical Rule to a dataset with a mean of 100 and a standard deviation of 5:
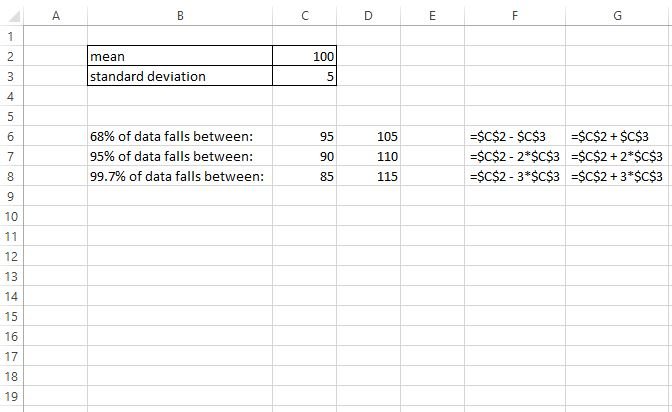
From this output, we can see:
- 68% of the data falls between 95 and 105
- 95% of the data falls between 90 and 110
- 99.7% of the data falls between 85 and 115
Finding What Percentage of Data Falls Between Certain Values
Another question you might have is: What percentage of data falls between certain values?
For example, suppose you have a normally-distributed dataset with a mean of 100, a standard deviation of 5, and you want to know what percentage of the data falls between the values 99 and 105.
In Excel, we can easily answer this question by using the function = NORM.DIST(), which takes the following arguments:
NORM.DIST(x, mean, standard_dev, cumulative)
where:
- x is the value we’re interested in
- mean is the mean of the distribution
- standard_dev is the standard deviation of the distribution
- cumulative takes a value of “TRUE” (returns the CDF) or “FALSE” (returns the PDF) – we’ll use “TRUE” to get the value of the cumulative distribution function.
The following screenshot shows how to use the NORM.DIST() function to find the percentage of the data that falls between the values 99 and 105 for a distribution that has a mean of 100 and a standard deviation of 5:
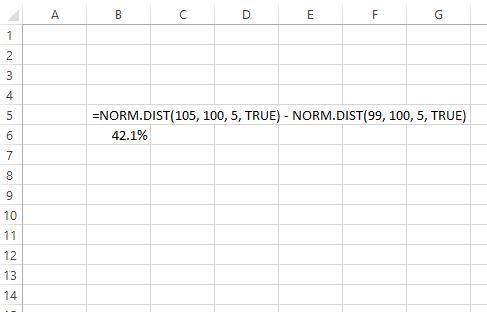
We see that 42.1% of the data falls between the values 105 and 99 for this distribution.
Helpful Tools:
Empirical Rule Calculator
Empirical Rule (Practice Problems)
