SciPy Spatial

The scipy.spatial package can calculate Triangulation, Voronoi Diagram and Convex Hulls of a set of points, by leveraging the Qhull library. Likewise, it contains KDTree implementations for nearest-neighbor point queries and utilities for distance computations in various metrics.

• Delaunay Triangulations

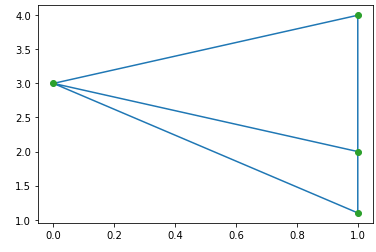
In mathematics and computation geometry, The Delaunay Triangulation defines that the three points from the triangle create a vertex when these vertex touch the path of the circle.

The center of the circle is determined by the radius of the three points or the triangle. Let us consider the following example:

Output:

Coplaner Points

Coplaner points are three or more points exist in the same plane. The plane is a flat surface, which can expand without end in all directions. Let us consider the following example:

Output:

[[4 0 3]]  

In the above output, point 4 is not included in the triangulation; it exists near triangle 0 and vertex 3.

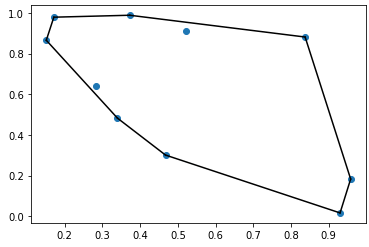
Convex hulls

In mathematics, the convex hull or convex envelope of a set of points X in Euclidean plan or in a Euclidean space. It is the smallest convex set that contains X. Let us consider the following example:

Output:

Scipy cdist

The SciPy provides the spatial.distance.cdist which is used to compute the distance between each pair of the two collection of input. The following are the calling conventions:

1. Y = cdist(XA, XB, ‘euclidean’)

It calculates the distance between m points using Euclidean distance (2-norm) as the distance metric between the points. The points are organized as m n-dimensional row vectors in the matrix X.

2. Y = cdist(XA, XB, ‘minkowski’, p=2.)

It calculates the distances using the Minkowski distance ||u?v||p (p-norm) where p?1.

3. Y = cdist(XA, XB, ‘cityblock’)

It calculates the city block or Manhattan distance between the points.