XOR gate
The XOR gate stands for the Exclusive-OR gate. This gate is a special type of gate used in different types of computational circuits. Apart from the AND, OR, NOT, NAND, and NOR gate, there are two special gates, i.e., Ex-OR and Ex-NOR. These gates are not basic gates in their own and are constructed by combining with other logic gates. Their Boolean output function is significant enough to be considered as a complete logic gate. The XOR and XNOR gates are the hybrids gates.
The 2-input OR gate is also known as the Inclusive-OR gate because when both inputs A and B are set to 1, the output comes out 1(high). In the Ex-OR function, the logic output “1” is obtained only when either A=”1″ or B=”1″ but not both together at the same time. Simply, the output of the XOR gate is high(1) only when both the inputs are different from each other.
The plus(+) sign within the circle is used as the Boolean expression of the XOR gate. So, the symbol of the XOR gate is ⨁. This Ex-OR symbol also defines the “direct sum of sub-objects” expression. These are the following types of Exclusive-OR gate:
2-input Ex-OR gate
This is a simple form of the hybrid gate XOR. In this type of XOR gate, there are only two input values and an output value. There are 22=4 possible combinations of inputs. The output level is high when both inputs are set to a different logic level. The Boolean expression of 2-input XOR gate is as follows:
Y=(A’ B+AB’)
The truth table and logic design are given below:
Logic Design
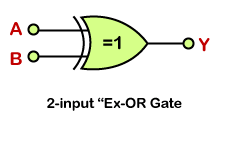
Truth Table
| Input | Output | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
The 3-input XOR Gate
Unlike the 2-input XOR gate, the 3-input XOR gate has three inputs. There are 23=8 possible combinations of inputs. The Boolean expression of the logical Ex-OR gate is as follows:
Y=A(BC)’+A’ BC’+(AB)’ C+ABC
The truth table and logic design are given below:
Logic Design
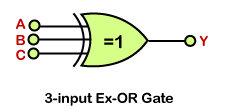
Truth Table
| Input | Output | ||
|---|---|---|---|
| A | B | C | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Ex-OR gate equivalent circuit
We can form the XOR or Ex-OR gate using gates such as AND, OR, and a universal gate NAND. The main disadvantage of this implementation is that we need to use different types of gates to form a single XOR gate. By using only the NAND gate, we can implement the Ex-OR gate also. This is an easier way of producing Ex-OR gate functionality.
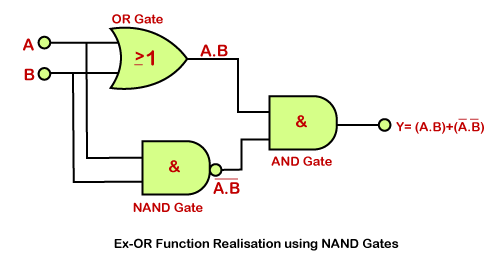
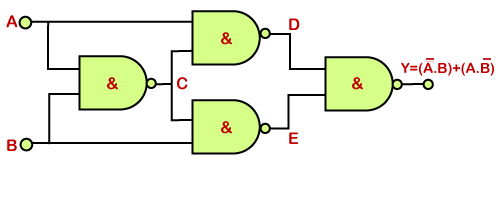
Use of Ex-OR gate
The Ex-or gate plays an important role in constructing digital circuits that perform arithmetic operations and calculations. Especially Adders and Half-Adders, as they can provide a “carry-bit” function or as a controlled inverter, where one input passes the binary data, and the other input is supplied with a control signal.
