Bayes’ theorem in Artificial intelligence
Bayes’ theorem:
Bayes’ theorem is also known as Bayes’ rule, Bayes’ law, or Bayesian reasoning, which determines the probability of an event with uncertain knowledge.
In probability theory, it relates the conditional probability and marginal probabilities of two random events.
Bayes’ theorem was named after the British mathematician Thomas Bayes. The Bayesian inference is an application of Bayes’ theorem, which is fundamental to Bayesian statistics.
It is a way to calculate the value of P(B|A) with the knowledge of P(A|B).
Bayes’ theorem allows updating the probability prediction of an event by observing new information of the real world.
Example: If cancer corresponds to one’s age then by using Bayes’ theorem, we can determine the probability of cancer more accurately with the help of age.
Bayes’ theorem can be derived using product rule and conditional probability of event A with known event B:
As from product rule we can write:
Similarly, the probability of event B with known event A:
Equating right hand side of both the equations, we will get:

The above equation (a) is called as Bayes’ rule or Bayes’ theorem. This equation is basic of most modern AI systems for probabilistic inference.
It shows the simple relationship between joint and conditional probabilities. Here,
P(A|B) is known as posterior, which we need to calculate, and it will be read as Probability of hypothesis A when we have occurred an evidence B.
P(B|A) is called the likelihood, in which we consider that hypothesis is true, then we calculate the probability of evidence.
P(A) is called the prior probability, probability of hypothesis before considering the evidence
P(B) is called marginal probability, pure probability of an evidence.
In the equation (a), in general, we can write P (B) = P(A)*P(B|Ai), hence the Bayes’ rule can be written as:
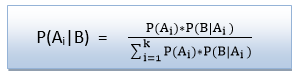
Where A1, A2, A3,…….., An is a set of mutually exclusive and exhaustive events.
Applying Bayes’ rule:
Bayes’ rule allows us to compute the single term P(B|A) in terms of P(A|B), P(B), and P(A). This is very useful in cases where we have a good probability of these three terms and want to determine the fourth one. Suppose we want to perceive the effect of some unknown cause, and want to compute that cause, then the Bayes’ rule becomes:
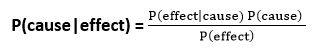
Example-1:
Question: what is the probability that a patient has diseases meningitis with a stiff neck?
Given Data:
A doctor is aware that disease meningitis causes a patient to have a stiff neck, and it occurs 80% of the time. He is also aware of some more facts, which are given as follows:
- The Known probability that a patient has meningitis disease is 1/30,000.
- The Known probability that a patient has a stiff neck is 2%.
Let a be the proposition that patient has stiff neck and b be the proposition that patient has meningitis. , so we can calculate the following as:
P(a|b) = 0.8
P(b) = 1/30000
P(a)= .02
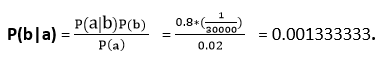
Hence, we can assume that 1 patient out of 750 patients has meningitis disease with a stiff neck.
Example-2:
Question: From a standard deck of playing cards, a single card is drawn. The probability that the card is king is 4/52, then calculate posterior probability P(King|Face), which means the drawn face card is a king card.
Solution:

P(king): probability that the card is King= 4/52= 1/13
P(face): probability that a card is a face card= 3/13
P(Face|King): probability of face card when we assume it is a king = 1
Putting all values in equation (i) we will get:

Application of Bayes’ theorem in Artificial intelligence:
Following are some applications of Bayes’ theorem:
- It is used to calculate the next step of the robot when the already executed step is given.
- Bayes’ theorem is helpful in weather forecasting.
- It can solve the Monty Hall problem.
