BFS vs. DFS
Before looking at the differences between BFS and DFS, we first should know about BFS and DFS separately.
What is BFS?
BFS stands for Breadth First Search. It is also known as level order traversal. The Queue data structure is used for the Breadth First Search traversal. When we use the BFS algorithm for the traversal in a graph, we can consider any node as a root node.
Let’s consider the below graph for the breadth first search traversal.
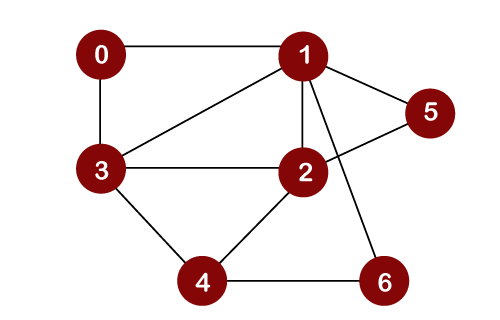
Suppose we consider node 0 as a root node. Therefore, the traversing would be started from node 0.

Once node 0 is removed from the Queue, it gets printed and marked as a visited node.
Once node 0 gets removed from the Queue, then the adjacent nodes of node 0 would be inserted in a Queue as shown below:

Now the node 1 will be removed from the Queue; it gets printed and marked as a visited node
Once node 1 gets removed from the Queue, then all the adjacent nodes of a node 1 will be added in a Queue. The adjacent nodes of node 1 are 0, 3, 2, 6, and 5. But we have to insert only unvisited nodes in a Queue. Since nodes 3, 2, 6, and 5 are unvisited; therefore, these nodes will be added in a Queue as shown below:

The next node is 3 in a Queue. So, node 3 will be removed from the Queue, it gets printed and marked as visited as shown below:

Once node 3 gets removed from the Queue, then all the adjacent nodes of node 3 except the visited nodes will be added in a Queue. The adjacent nodes of node 3 are 0, 1, 2, and 4. Since nodes 0, 1 are already visited, and node 2 is present in a Queue; therefore, we need to insert only node 4 in a Queue.

Now, the next node in the Queue is 2. So, 2 would be deleted from the Queue. It gets printed and marked as visited as shown below:

Once node 2 gets removed from the Queue, then all the adjacent nodes of node 2 except the visited nodes will be added in a Queue. The adjacent nodes of node 2 are 1, 3, 5, 6, and 4. Since the nodes 1 and 3 have already been visited, and 4, 5, 6 are already added in the Queue; therefore, we do not need to insert any node in the Queue.
The next element is 5. So, 5 would be deleted from the Queue. It gets printed and marked as visited as shown below:

Once node 5 gets removed from the Queue, then all the adjacent nodes of node 5 except the visited nodes will be added in the Queue. The adjacent nodes of node 5 are 1 and 2. Since both the nodes have already been visited; therefore, there is no vertex to be inserted in a Queue.
The next node is 6. So, 6 would be deleted from the Queue. It gets printed and marked as visited as shown below:

Once the node 6 gets removed from the Queue, then all the adjacent nodes of node 6 except the visited nodes will be added in the Queue. The adjacent nodes of node 6 are 1 and 4. Since the node 1 has already been visited and node 4 is already added in the Queue; therefore, there is not vertex to be inserted in the Queue.
The next element in the Queue is 4. So, 4 would be deleted from the Queue. It gets printed and marked as visited.
Once the node 4 gets removed from the Queue, then all the adjacent nodes of node 4 except the visited nodes will be added in the Queue. The adjacent nodes of node 4 are 3, 2, and 6. Since all the adjacent nodes have already been visited; so, there is no vertex to be inserted in the Queue.
What is DFS?
DFS stands for Depth First Search. In DFS traversal, the stack data structure is used, which works on the LIFO (Last In First Out) principle. In DFS, traversing can be started from any node, or we can say that any node can be considered as a root node until the root node is not mentioned in the problem.
In the case of BFS, the element which is deleted from the Queue, the adjacent nodes of the deleted node are added to the Queue. In contrast, in DFS, the element which is removed from the stack, then only one adjacent node of a deleted node is added in the stack.
Let’s consider the below graph for the Depth First Search traversal.
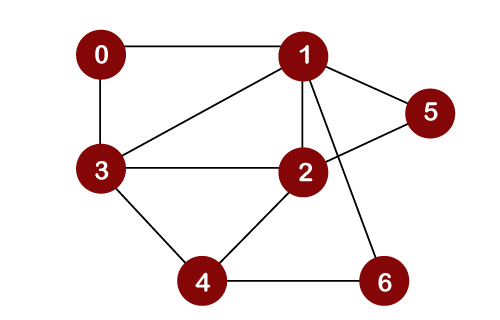
Consider node 0 as a root node.
First, we insert the element 0 in the stack as shown below:

The node 0 has two adjacent nodes, i.e., 1 and 3. Now we can take only one adjacent node, either 1 or 3, for traversing. Suppose we consider node 1; therefore, 1 is inserted in a stack and gets printed as shown below:

Now we will look at the adjacent vertices of node 1. The unvisited adjacent vertices of node 1 are 3, 2, 5 and 6. We can consider any of these four vertices. Suppose we take node 3 and insert it in the stack as shown below:

Consider the unvisited adjacent vertices of node 3. The unvisited adjacent vertices of node 3 are 2 and 4. We can take either of the vertices, i.e., 2 or 4. Suppose we take vertex 2 and insert it in the stack as shown below:

The unvisited adjacent vertices of node 2 are 5 and 4. We can choose either of the vertices, i.e., 5 or 4. Suppose we take vertex 4 and insert in the stack as shown below:

Now we will consider the unvisited adjacent vertices of node 4. The unvisited adjacent vertex of node 4 is node 6. Therefore, element 6 is inserted into the stack as shown below:

After inserting element 6 in the stack, we will look at the unvisited adjacent vertices of node 6. As there is no unvisited adjacent vertices of node 6, so we cannot move beyond node 6. In this case, we will perform backtracking. The topmost element, i.e., 6 would be popped out from the stack as shown below:

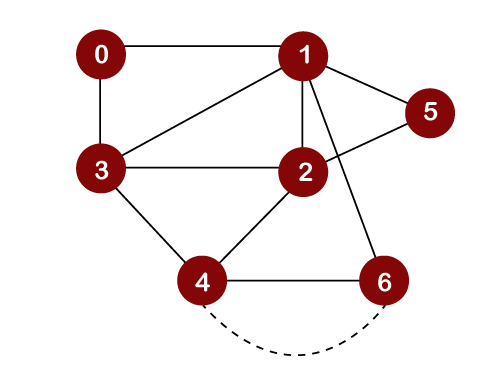
The topmost element in the stack is 4. Since there are no unvisited adjacent vertices left of node 4; therefore, node 4 is popped out from the stack as shown below:

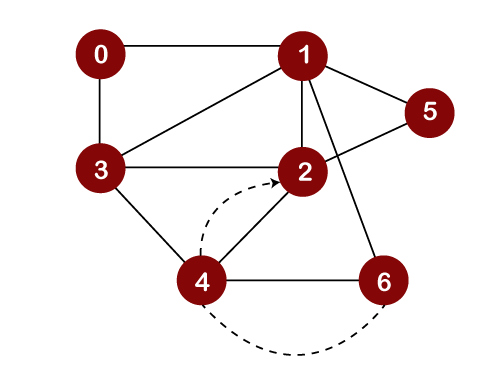
The next topmost element in the stack is 2. Now, we will look at the unvisited adjacent vertices of node 2. Since only one unvisited node, i.e., 5 is left, so node 5 would be pushed into the stack above 2 and gets printed as shown below:

Now we will check the adjacent vertices of node 5, which are still unvisited. Since there is no vertex left to be visited, so we pop the element 5 from the stack as shown below:

We cannot move further 5, so we need to perform backtracking. In backtracking, the topmost element would be popped out from the stack. The topmost element is 5 that would be popped out from the stack, and we move back to node 2 as shown below:
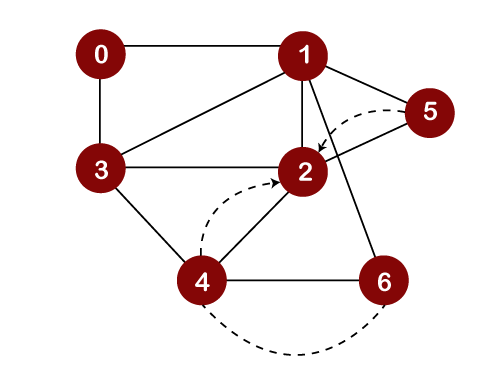
Now we will check the unvisited adjacent vertices of node 2. As there is no adjacent vertex left to be visited, so we perform backtracking. In backtracking, the topmost element, i.e., 2 would be popped out from the stack, and we move back to the node 3 as shown below:
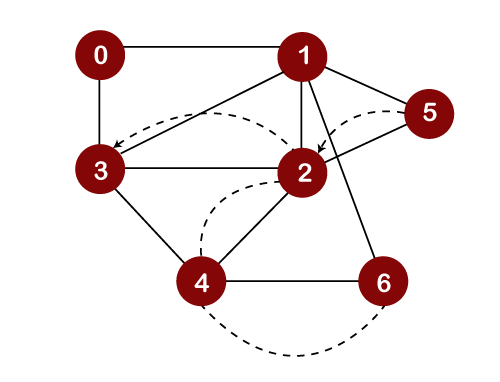

Now we will check the unvisited adjacent vertices of node 3. As there is no adjacent vertex left to be visited, so we perform backtracking. In backtracking, the topmost element, i.e., 3 would be popped out from the stack and we move back to node 1 as shown below:

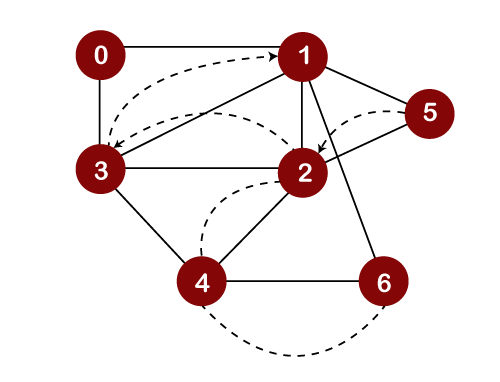
After popping out element 3, we will check the unvisited adjacent vertices of node 1. Since there is no vertex left to be visited; therefore, the backtracking will be performed. In backtracking, the topmost element, i.e., 1 would be popped out from the stack, and we move back to node 0 as shown below:

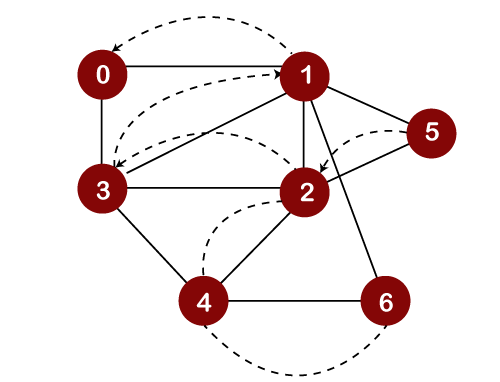
We will check the adjacent vertices of node 0, which are still unvisited. As there is no adjacent vertex left to be visited, so we perform backtracking. In this, only one element, i.e., 0 left in the stack, would be popped out from the stack as shown below:

As we can observe in the above figure that the stack is empty. So, we have to stop the DFS traversal here, and the elements which are printed is the result of the DFS traversal.
Differences between BFS and DFS
The following are the differences between the BFS and DFS:
| BFS | DFS | |
|---|---|---|
| Full form | BFS stands for Breadth First Search. | DFS stands for Depth First Search. |
| Technique | It a vertex-based technique to find the shortest path in a graph. | It is an edge-based technique because the vertices along the edge are explored first from the starting to the end node. |
| Definition | BFS is a traversal technique in which all the nodes of the same level are explored first, and then we move to the next level. | DFS is also a traversal technique in which traversal is started from the root node and explore the nodes as far as possible until we reach the node that has no unvisited adjacent nodes. |
| Data Structure | Queue data structure is used for the BFS traversal. | Stack data structure is used for the BFS traversal. |
| Backtracking | BFS does not use the backtracking concept. | DFS uses backtracking to traverse all the unvisited nodes. |
| Number of edges | BFS finds the shortest path having a minimum number of edges to traverse from the source to the destination vertex. | In DFS, a greater number of edges are required to traverse from the source vertex to the destination vertex. |
| Optimality | BFS traversal is optimal for those vertices which are to be searched closer to the source vertex. | DFS traversal is optimal for those graphs in which solutions are away from the source vertex. |
| Speed | BFS is slower than DFS. | DFS is faster than BFS. |
| Suitability for decision tree | It is not suitable for the decision tree because it requires exploring all the neighboring nodes first. | It is suitable for the decision tree. Based on the decision, it explores all the paths. When the goal is found, it stops its traversal. |
| Memory efficient | It is not memory efficient as it requires more memory than DFS. | It is memory efficient as it requires less memory than BFS. |
