Binary Search Algorithm
In this article, we will discuss the Binary Search Algorithm. Searching is the process of finding some particular element in the list. If the element is present in the list, then the process is called successful, and the process returns the location of that element. Otherwise, the search is called unsuccessful.
Linear Search and Binary Search are the two popular searching techniques. Here we will discuss the Binary Search Algorithm.
Binary search is the search technique that works efficiently on sorted lists. Hence, to search an element into some list using the binary search technique, we must ensure that the list is sorted.
Binary search follows the divide and conquer approach in which the list is divided into two halves, and the item is compared with the middle element of the list. If the match is found then, the location of the middle element is returned. Otherwise, we search into either of the halves depending upon the result produced through the match.
NOTE: Binary search can be implemented on sorted array elements. If the list elements are not arranged in a sorted manner, we have first to sort them.
Now, let’s see the algorithm of Binary Search.
Algorithm
Working of Binary search
Now, let’s see the working of the Binary Search Algorithm.
To understand the working of the Binary search algorithm, let’s take a sorted array. It will be easy to understand the working of Binary search with an example.
There are two methods to implement the binary search algorithm –
- Iterative method
- Recursive method
The recursive method of binary search follows the divide and conquer approach.
Let the elements of array are –

Let the element to search is, K = 56
We have to use the below formula to calculate the mid of the array –
So, in the given array –
beg = 0
end = 8
mid = (0 + 8)/2 = 4. So, 4 is the mid of the array.
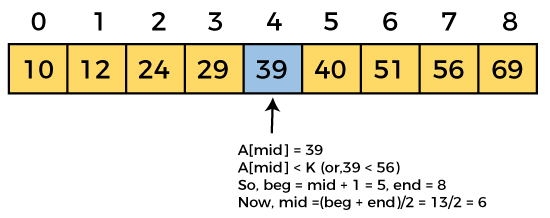
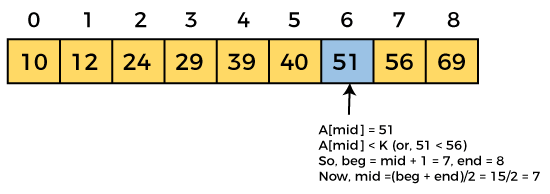
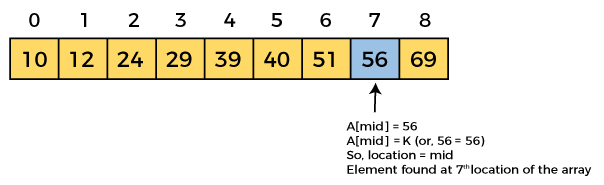
Now, the element to search is found. So algorithm will return the index of the element matched.
Binary Search complexity
Now, let’s see the time complexity of Binary search in the best case, average case, and worst case. We will also see the space complexity of Binary search.
1. Time Complexity
| Case | Time Complexity |
|---|---|
| Best Case | O(1) |
| Average Case | O(logn) |
| Worst Case | O(logn) |
- Best Case Complexity – In Binary search, best case occurs when the element to search is found in first comparison, i.e., when the first middle element itself is the element to be searched. The best-case time complexity of Binary search is O(1).
- Average Case Complexity – The average case time complexity of Binary search is O(logn).
- Worst Case Complexity – In Binary search, the worst case occurs, when we have to keep reducing the search space till it has only one element. The worst-case time complexity of Binary search is O(logn).
2. Space Complexity
| Space Complexity | O(1) |
- The space complexity of binary search is O(1).
Implementation of Binary Search
Now, let’s see the programs of Binary search in different programming languages.
Program: Write a program to implement Binary search in C language.
Output

Program: Write a program to implement Binary search in C++.
Output
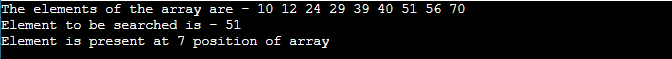
Program: Write a program to implement Binary search in C#.
Output

Program: Write a program to implement Binary search in Java.
Output
Program: Write a program to implement Binary search in PHP.
Output

So, that’s all about the article. Hope the article will be helpful and informative to you.
