Cocktail Sort Algorithm

In this article, we will discuss the cocktail sort algorithm. Cocktail sort is the variation of Bubble Sort, which traverses the list in both directions alternatively. It is different from bubble sort in the sense that bubble sort traverses the list in the forward direction only, while this algorithm traverses in forward as well as backward direction in one iteration.

Cocktail sort is also called as bi-directional bubble sort. In bubble sort, elements are traversed from left to right, i.e., in one direction. In first iteration, bubble sort first moves the largest element to its correct position, then the second-largest element in its exact position, and so on. But cocktail sort traverses in both directions alternatively.

As similar to the bubble sort, the worst and average case complexities of cocktail sort is O(n²). Cocktail sort is faster than bubble sort.

There are two stages of cocktail sort in one iteration that are listed as follows –

In first stage, similar to the bubble sort, loop through the array from left to right. The adjacent elements are compared, and if the left element is greater than the right one, we swap those elements. The largest element of the list is placed at the end of the array in the forward pass.
In second stage, loop through the array from the rightmost unsorted element to the left. The adjacent elements are compared, and if the right element is smaller than the left element then, we swap those elements. The smallest element of the list is placed at the beginning of the array in the backward pass.

This process continues until the array elements are not sorted.

Now, let’s see the algorithm of cocktail sort algorithm.

Algorithm

  cocktailSort(a, n) // ‘a’ is the given array, ‘n’ is the size of given array  swapped = true  beg = 0  end = n-1  while(swapped)  swapped = false  for i in range from beg to end  if (a[i] > a[i + 1])  swap(a[i], a[i+1])  swapped = true  End if  End for loop  if(!swapped)  break  end if  swapped = false  end = end – 1  for i in range from end – 1 to beg  if (a[i] > a[i + 1])  swap(a[i], a[i+1])  swapped = true  End if  End for loop  start = start + 1  End while loop  End cocktailSort  

Working of Cocktail Sort Algorithm

Now, let’s see the working of the cocktail sort Algorithm.

To understand the working of the cocktail sort algorithm, let’s take an unsorted array. We are taking a short and accurate array, as we know the complexity of the cocktail sort is O(n²).

Let the elements of array are –

Array = {4, 0, 3, 1, 7, 1, 2}

Iteration 1:

First Forward pass:

In first iteration, the forward pass is similar to the bubble sort. The comparisons of forward pass in first iteration are given as follows –

Sorting will start from the initial two elements. Let compare them to check which is greater.

After swapping new array will look like –

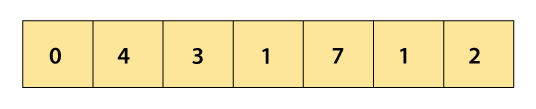
Now compare 4 and 3.

After swapping new array will look like –

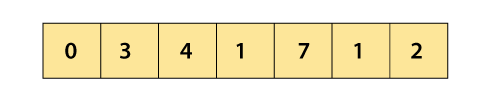
Now, compare 4 and 1.

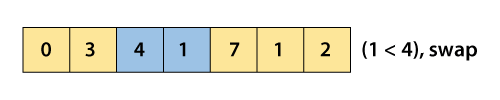
After swapping new array will look like –

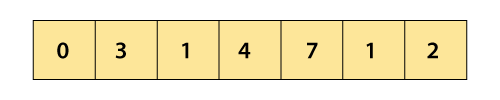
Now, compare 4 and 7.

Now, the comparison will be between 7 and 1.

After swapping new array will look like –

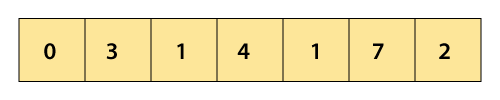
Now, compare 7 and 2.

Now, we reach at the end of the array. After swapping and first forward pass, the array elements will look like –

After the first forward pass, the largest element of the array is stored at the last position of the array.

First Backward pass:

Now, the first backward pass is started. It will be started from the last index of the array except for the index where the largest element is stored.

So, from the backward direction, first array elements 2 and 1 will be compared.

Now compare, 1 and 4.

After swapping, the array will be –

Now compare 1 and 1.

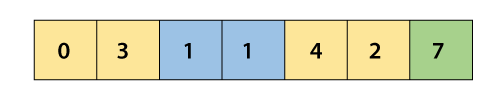
Now compare, 3 and 1.

After swapping, the array will be –

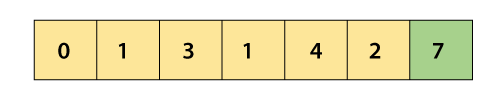
Now compare, 0 and 1.

So, after the first backward pass, smallest element from the array is stored at the first index of array. So, after first iteration, the array elements will be –

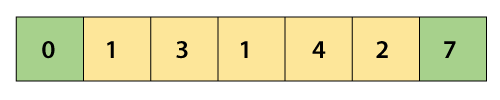
Iteration 2:

Second Forward pass:

Now, the second forward pass is started. It will be started from the first index of the array except for the index where the smallest element is stored.

So, from the forward direction, first array elements 1 and 3 will be compared.

Now, we reach at the end of the array. After the second forward pass, the second largest array element will be stored at its exact position. After swapping and second forward pass, the array elements will look like –

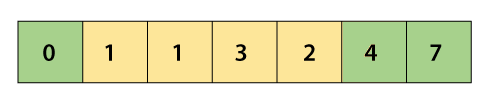
Second Backward pass:

Now, the second backward pass is started.

So, from backward direction, array elements 3 and 2 will be compared.

After swapping, the array will be –

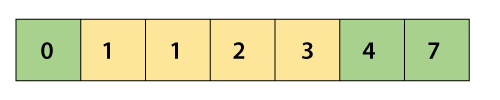
Now, the array is completely sorted, but the algorithm has to complete the entire pass without any swap to know that the array is sorted.

So, after sorting the array elements will be –

Now, the array is completely sorted.

Cocktail sort complexity

Now, let’s see the time complexity of cocktail sort in the best case, average case, and worst case. We will also see the space complexity of the cocktail sort.

1. Time Complexity

Case	Time Complexity
Best Cased	O(n)
Average Case	O(n²)
Worst Case	O(n²)

Best Case Complexity – It occurs when there is no sorting required, i.e., the array is already sorted. The best-case time complexity of cocktail sort is O(n).
Average Case Complexity – It occurs when the array elements are in jumbled order that is not properly ascending and not properly descending. The average case time complexity of cocktail sort is O(n²).
Worst Case Complexity – It occurs when the array elements are required to be sorted in reverse order. That means suppose you have to sort the array elements in ascending order, but its elements are in descending order. The worst-case time complexity of cocktail sort is O(n²).

2. Space Complexity

Space Complexity	O(1)
Stable	YES

The space complexity of the cocktail sort is O(1).

Implementation of cocktail sort

Now, let’s see the programs of cocktail sort in different programming languages.

Program: Write a program to implement cocktail sort in C language.

  #include     /* function to implement Cocktail sort */  void cocktail(int a[], int n)  {  int swap = 1;  int beg = 0;  int end = n – 1;      int i, temp;  while (swap)  {  swap = 0;    /* Loop similar to bubble sort to compare and swap array elements starting from left to right */  for (i = beg; i < end; ++i)  {  if (a[i] > a[i + 1]) {      temp = a[i];        a[i] = a[i+1];        a[i+1] = temp;         swap = 1;  }  }    if (!swap)  break;    swap = 0;    /* decrease the ‘end’ point by one position.   It is because the item at the last position is at its correct position */  –end;     /* This loop starts from right to left to perform the same comparison as in the previous loop */  for (int i = end – 1; i >= beg; –i)  {  if (a[i] > a[i + 1]) {      temp = a[i];        a[i] = a[i+1];        a[i+1] = temp;         swap = 1;  }  }    /* increase the beg point by one position.   It is because the item at the first position is at its correct position */  ++beg;  }  }     void print(int a[], int n) //function to print array elements      {      int i;      for(i = 0; i < n; i++)        {            printf(“%d “, a[i]);        }            }      int main()  {      int a[] = { 40, 10, 30, 5, 70, 2, 20 };         int n = sizeof(a)/sizeof(a[0]);       printf(“Before sorting array elements are – n”);      print(a, n);      cocktail(a, n);      printf(“nAfter sorting array elements are – n”);        print(a, n);      return 0;  }  

Output:

Program: Write a program to implement cocktail sort in C++.

  #include     using namespace std;    /* function to implement Cocktail sort */  void cocktail(int a[], int n)  {  int swap = 1;  int beg = 0;  int end = n – 1;      int i, temp;  while (swap)  {  swap = 0;    /* Loop similar to bubble sort to compare and swap array elements starting from left to right */  for (i = beg; i < end; ++i)  {  if (a[i] > a[i + 1]) {      temp = a[i];        a[i] = a[i+1];        a[i+1] = temp;         swap = 1;  }  }    if (!swap)  break;    swap = 0;    /* decrease the ‘end’ point by one position.   It is because the item at the last position is at its correct position */  –end;     /* This loop starts from right to left to perform the same comparison as in the previous loop */  for (int i = end – 1; i >= beg; –i)  {  if (a[i] > a[i + 1]) {      temp = a[i];        a[i] = a[i+1];        a[i+1] = temp;         swap = 1;  }  }    /* increase the beg point by one position.   It is because the item at the first position is at its correct position */  ++beg;  }  }     void print(int a[], int n) //function to print array elements      {      int i;      for(i = 0; i < n; i++)        {            cout<<a a="" are="" array="" cocktail="" cout="" elements="" int="" main="" n="sizeof(a)/sizeof(a[0]);" print="" return="" sorting="" textarea=""></a>[i]

Output:

Program: Write a program to implement cocktail sort in C#.

  using System;  class CocktailSort {    /* function to implement Cocktail sort */  static void cocktail(int[] a, int n)  {  int swap = 1;  int beg = 0;  int end = n – 1;      int i, temp;  while (swap == 1)  {  swap = 0;    /* Loop similar to bubble sort to compare and swap array elements starting from left to right */  for (i = beg; i < end; ++i)  {  if (a[i] > a[i + 1]) {      temp = a[i];        a[i] = a[i+1];        a[i+1] = temp;         swap = 1;  }  }    if (swap == 0)  break;    swap = 0;    /* decrease the ‘end’ point by one position.   It is because the item at the last position is at its correct position */  –end;     /* This loop starts from right to left to perform the same comparison as in the previous loop */  for (i = end – 1; i >= beg; –i)  {  if (a[i] > a[i + 1]) {      temp = a[i];        a[i] = a[i+1];        a[i+1] = temp;         swap = 1;  }  }    /* increase the beg point by one position.   It is because the item at the first position is at its correct position */  ++beg;  }  }     static void print(int[] a, int n) //function to print array elements      {      int i;      for(i = 0; i < n; i++)        {            Console.Write(a[i] + ” “);        }            }      static void Main()   {      int[] a = { 38, 4, 28, 3, 68, 0, 18 };         int n = a.Length;       Console.Write(“Before sorting array elements are – n”);      print(a, n);      cocktail(a, n);      Console.Write(“nAfter sorting array elements are – n”);        print(a, n);  }  }  

Output:

Program: Write a program to implement cocktail sort in Java.

  class CocktailSort {    /* function to implement Cocktail sort */  static void cocktail(int a[], int n)  {  int swap = 1;  int beg = 0;  int end = n – 1;      int i, temp;  while (swap == 1)  {  swap = 0;    /* Loop similar to bubble sort to compare and swap array elements starting     from left to right */  for (i = beg; i < end; ++i)  {  if (a[i] > a[i + 1]) {      temp = a[i];        a[i] = a[i+1];        a[i+1] = temp;         swap = 1;  }  }    if (swap == 0)  break;    swap = 0;    /* decrease the ‘end’ point by one position.   It is because the item at the last position is at its     correct position */  –end;     /* This loop starts from right to left to perform the     same comparison as in the previous loop */  for (i = end – 1; i >= beg; –i)  {  if (a[i] > a[i + 1]) {      temp = a[i];        a[i] = a[i+1];        a[i+1] = temp;         swap = 1;  }  }    /* increase the beg point by one position.   It is because the item at the first position is at its     correct position */  ++beg;  }  }     static void print(int a[], int n) //function to print array elements      {      int i;      for(i = 0; i < n; i++)        {            System.out.print(a[i] + ” “);        }            }      public static void main(String args[])   {      int[] a = { 37, 3, 27, 2, 67, 0, 17 };         int n = a.length;       System.out.print(“Before sorting array elements are – n”);      print(a, n);      cocktail(a, n);      System.out.print(“nAfter sorting array elements are – n”);        print(a, n);  }  }  

Output:

So, that’s all about the article. Hope the article will be helpful and informative to you.

Next TopicCycle Sort

Cocktail Sort

Cocktail Sort Algorithm

Algorithm

Working of Cocktail Sort Algorithm

Cocktail sort complexity

1. Time Complexity

2. Space Complexity

Implementation of cocktail sort

DS Array representation of Queue

DS | Array vs linked list

You may also like