Complement Naive Bayes (CNB) Algorithm
Naive Bayes algorithms are one of a number of highly popular and commonly utilized Machine Learning algorithms used for classification. There are numerous ways that the Naive Bayes algorithm is applied, such as Gaussian Naive Bayes, Multinomial Naive Bayes, and so on.
Complement Naive Bayes is somewhat a modification of the standard Multinomial Naive Bayes algorithm. Multinomial Naive Bayes is not able to do very well with unstable data. Imbalanced data sets are instances where the number of instances belonging to a particular class is greater than the number of instances belonging to different classes. This implies the spread of the examples is not even. This kind of data can be difficult to analyse as models can easily overfit this data to benefit a class with a larger instance.
How CNB Works:
Complement Naive Bayes is particularly suited to deal with data that is imbalanced. In Complement Naive Bayes, instead of calculating the probability of an item belonging to a specific class, we calculate the probability of an item being part of all classes. That is what the term means in its literal sense complement and thus is referred to as Complement Naive Bayes.
A step-by-step overview of the algorithm (without any maths involved):
- Calculate the likelihood of the instance not being part of it for each class.
- After we calculate all classes, we review all the calculated values and pick the smallest value.
- The most minimal value (lowest chance) is chosen because it has the lowest chance that it does not belong to the class in question. This means it is most likely to be part of the class. This is why this class is chosen.
Let’s consider an example: For instance, there are two types of classes: Apples and Bananas, and we need to determine if a sentence is connected to bananas or apples in light of that the word frequency is a particular number of words. Here is a table-based representation of the basic dataset:
| S. No. | Round | Red | Long | Yellow | Soft | Class |
|---|---|---|---|---|---|---|
| 1 | 2 | 1 | 1 | 0 | 0 | Apples |
| 2 | 1 | 1 | 3 | 9 | 6 | Bananas |
| 3 | 3 | 4 | 0 | 0 | 1 | Apples |
| 4 | 2 | 3 | 1 | 1 | 0 | Apples |
Total word count in class ‘Apples’ = (2+1+1) + (3+4+1) + (2 + 3 + 1 + 1) = 19
Total word count in class ‘Bananas’ = (1 + 1 + 3 + 9 + 6) = 20
So, the Probability of a sentence to belong to the class, ‘Apples’:
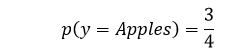
Likewise, the probability of a sentence to belong to the class, ‘Bananas’,
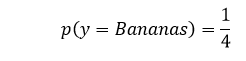
In the table above, we have represented an array of data. The columns indicate how many words are used within the sentence and determine which category the sentence is part of. Before we get started with the data, we must first learn about Bayes Theorem.
Bayes Theorem can be utilized to calculate the likelihood of an given that another event takes place. The formula is:
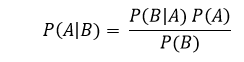
In the case of A and B being two events, P(A) is the likelihood of occurring of A. P(A|B) is the chance for A occurring in the event that has already occurred. P(B) means that the chance of an event happening can’t be zero since it already happened.
Now let’s look at the way Naive Bayes is used and how Complement Naive Bayes operates. The standard Naive Bayes algorithm works:
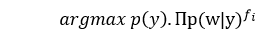
where “fi” is frequency of some attribute. For instance, the number of times specific words appear in the same sentence.
To complement Naive Bayes, the formula is
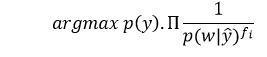
When we have a close examine the formulae, we will notice how the complement Naive Bayes is essentially the opposite of normal Naive Bayes. CNB formula will be the class that is predicted. In Naive Bayes, the class that has the largest value derived by the formula will be the one that will be predicted. Also, as Complement Naive Bayes is just the reverse of the CNB formula, the class with the lowest value calculated by the CNB formula is the predicted class.
Now, let’s look at an example of a shopper and attempt to model it by using our CNB and our data,
| Round | Red | Long | Yellow | Soft | Class |
|---|---|---|---|---|---|
| 2 | 2 | 0 | 1 | 1 | ? |
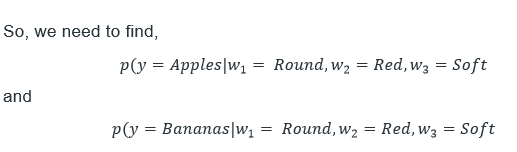
It is necessary to evaluate the numbers and choose the expected class with the lower value. It is necessary to do this for bananas and select the class with the lowest value. i.e., If we have a value of (y equals Apples) is lower than it is predicted to be Apples; however, if it is the case that (y = bananas) is less than the value for (y = Apples), the class is forecast as Bananas.
Utilizing this formula, we can use the Complement Naive Bayes Formula for both classes.
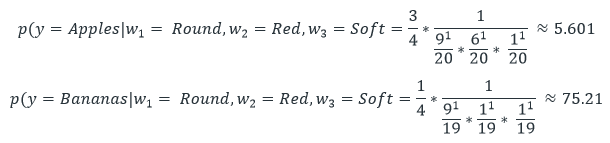
In the present, as 5.601 < 75.213, The predicted class would be Apples.
We don’t employ the class with the highest value since higher values mean there is a higher probability the sentence that contains these words is not related to that class. This is the reason this algorithm is referred to as “complement” Naive Bayes.
When should we use CNB?
- If the data set that the classification will be performed is not balanced, the Multinomial, as well as Gaussian Naive Bayes, might yield low accuracy. Yet, Complement Naive Bayes will be quite effective and offer a much higher accuracy.
- To classify text for text classification: The Complement Naive Bayes outperforms both Gaussian Naive Bayes and Multinomial Naive Bayes in text classification tasks.
Implementation of CNB within Python:
In this case, we will be using the wine dataset, which is slightly off. It determines the source of wine based on different chemical parameters. To learn more about this data set, go to the link.
To assess our model, we’ll verify the accuracy of the test set as well as the report on the classification of the classifier. We will utilize the scikit-learn library for implementing our Complement Naive Bayes algorithm.
Code:
Output:
Accuracy of Training Set: 65.41353383458647 % Accuracy of Test Set: 60.0 % Classifier Report : precision recall f1-score support 0 0.67 0.92 0.77 13 1 0.56 0.88 0.68 17 2 0.00 0.00 0.00 15 accuracy 0.60 45 macro avg 0.41 0.60 0.49 45 weighted avg 0.40 0.60 0.48 45
We can get an accuracy rate of 65.41 percent for the training set, and the accuracy is 60.00 percent on the testing set. These are the same and quite high given the high quality of the data. The data is known because it is difficult to identify using simple classifiers like those we’ve applied in this case. So, the accuracy is acceptable.
Conclusion
We now know the basics of Complement Naive Bayes classifiers and how they function when we find ourselves in an unbalanced dataset, test employing Complement Naive Bayes.
