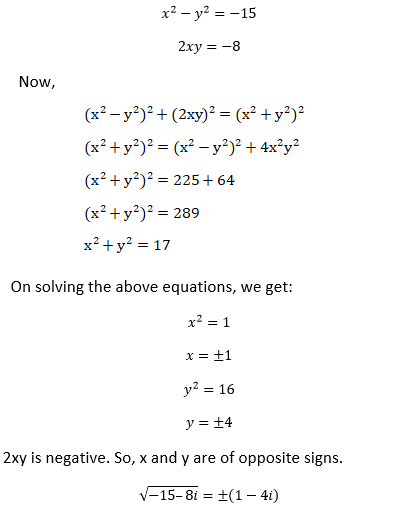Complex Numbers
The equation of the form x^2 + 4 = 2 or x^2 + 1 = 0 is not solvable because there exists no rational number whose square is -2 or -1. Euler was the mathematician who first introduced the term iota for the square root of negative numbers (example -1). The iota symbol was further derived as the imaginary unit. The mathematician calculated the solution of the equation x^2 + 1 = 0 with the property i^2 = -1.
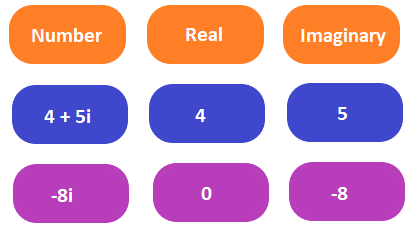
Complex numbers signify the combination of real and imaginary parts in a number.
Let’s first discuss what real and imaginary numbers are.
Real numbers
Real numbers are the numbers in the form of a fraction, integers, and irrational numbers. For example,

Imaginary Numbers
Imaginary numbers are the numbers that include iota. The square of imaginary numbers is a negative number.
For example,

It is because the square of iota is equal to -1. The examples of imaginary numbers are:

Thus, complex numbers can be represented as:
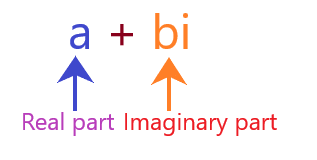
Where,
a and b are the two real numbers.
The number with the term iota is called an imaginary part of the number. The non-iota part is known as a real part of that number. A number with no real part is called a purely imaginary number. Similarly, a number with no real part is called a purely real number.
For example,
Visual Representation of Complex Numbers
Let’s understand the complex numbers in the visual form.
The two axes on a graph are the real axis and imaginary axis, as shown below:
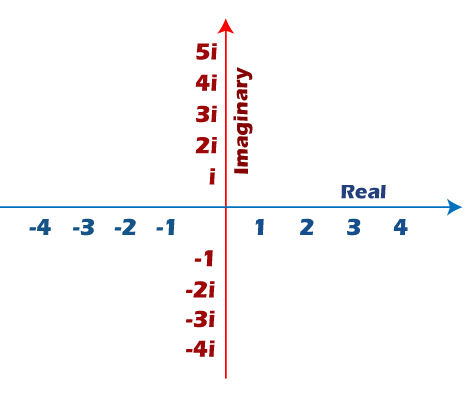
The complex number z = a + ib can be represented as follows:
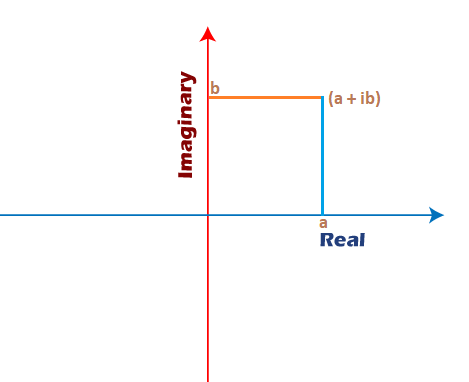
Here, a and b are the numbers on the real and imaginary axis.
Let’s represents some complex numbers on the above graph.
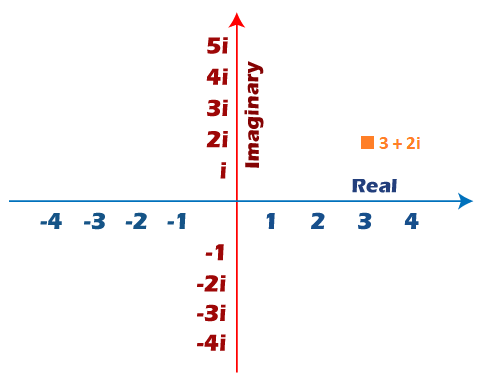
1. 3 + 2i
The coordinates of the given complex number are (3, 2). Here, the number 3 lies on the real axis, and 2 lies on the imaginary axis, as shown below:
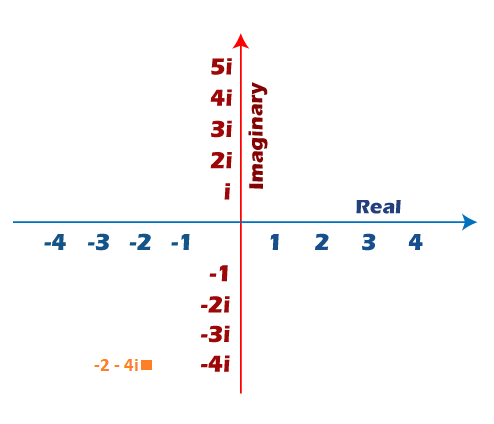
2. -2 – 4i
The coordinates of the given complex number are (-2, -4). Here, the number -2 lies on the real axis, and -4 lies on the imaginary axis, as shown below:
Numbers are categorized as real and complex. A number consists of two parts, i.e., real and imaginary. The real numbers consist of only real parts, while the complex number consists of real and imaginary parts.
The square of an imaginary part is negative, while the square of the real part is positive. For example,

We can also say that the square root of a negative number is an imaginary quantity.
Power of Iota
Here, we will discuss the positive and negative powers of the iota (i).
Positive powers of i:
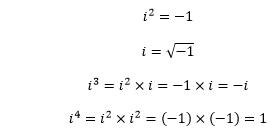
Thus, we can say that:
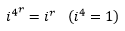
Negative powers of i:
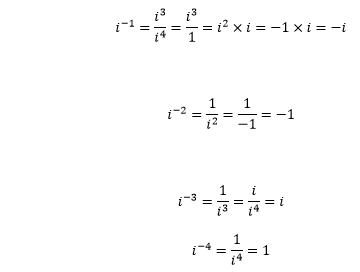
Let’s evaluate the higher powers of iota.
The higher power of iota can be easily calculated with the help of these above four positive powers.
Example: Evaluate the following powers of iota given below:
(a)=i-999
(b)=i135
Solution:
(a) We know,
i4=1
When we divide 999 by 4, we get 3 as a remainder.
We can write it as:
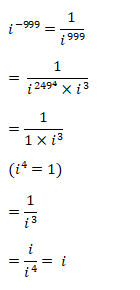
(b) When we divide 135 by 4, we get 3 as a remainder.
We can write it as:
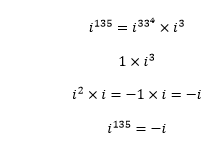
Equality of Complex Numbers
Let the two complex numbers be z1 and z2.
If, z1 = a1 + ib1
z2 = a2 +ib2
The above complex numbers are equal, if a1 = a2 and b1 = b2.
It means the Real part of z1 = Real part of z2, and the Imaginary part of z1 = imaginary part of z2.
Let’s understand it with few examples.
Example 1: If, z1 = 4 – iy and z2 = x + 5i are equal, find the value of x and y.
Given: z1 = z2.
4 – iy = x + 5i
We know, Re (z1) = Re (z2)
After comparing, we get,
x = 4
Similarly, equating Im (z1) = Im (z2)
We get,
y = -5 or -y = 5
Example 2: Find the value of a and b, if:
(a + b) – i (3a + 2b) = 5 + 2i
After equating the real and imaginary parts, we get:
a + b = 5 and 3a + 2b = 2
Solving the above two equations, we get:
a = -12
b = 17
Addition of Complex Numbers
Let the two complex numbers be z1 and z2, where:
z1 = a1 + ib1
z2 = a2 +ib2
The addition of two complex numbers z1 and z2 is equal to the complex number (a1 +a2) + i (b1 + b2).
The real part of a first number is added with the real part of the second number. It means that the real part can be added to the real part of the other number.
Similarly, the imaginary part of a first number is added with the imaginary part of the second number.
Re (z1 + z2) = Re (z1) + Re (z2)
Im (z1 + z2) = Im (z1) + Im (z2)
Let’s consider few examples.
Example 1: If, z1 = (3x – 7) + 2iy and z2 = -5y + (5 + x) i. Find z1 + z2.
z1 + z2 = (3x – 7) + 2iy + (-5y + (5 + x) i)
z1 + z2 = 3x – 7 + 2iy – 5y + 5i + xi
z1 + z2 = 3x – 5y -7 + i(x + 2y + 5)
Example 2: If, z1 = 5 + 4i and z2 =6 – 2i. Find z1 + z2.
z1 + z2 = 5 + 4i + 6 -2i
z1 + z2 = 11 + 2i
Subtraction of Complex Numbers
Let the two complex numbers be z1 and z2, where:
z1 = a1 + ib1
z2 = a2 +ib2
The Subtraction of a complex number z2 from z1 is denoted as z1 – z2. We can also define it as the addition of two complex numbers z1 and -z2.
Similarly, the Subtraction of a complex number z1 from z2 is denoted as z2 – z1. It is also equal to z2 + (-z1).
Let’s consider some examples.
Example 1: Find z1 – z2, if z1 = 5 + 3i and z2 = 2 – 7i.
z1 – z2 = 5 + 3i – (2 – 7i)
= 5 + 3i – 2 + 7i
= 3 + 10i
z1 – z2 = 3 + 10i
Example 2: Find z1 – z2, if z1 = 4 + 3i (2i + 7) and z2 = 2 – 7i (2i + 6).
z1 – z2 = 4 + 3i (2i – 7) – [2 – 7i (2i + 6)]
z1 – z2 = 4 + 6i^2 – 21i – [2 – 14i^2 – 42i]
z1 – z2 = 4 + 6i^2 – 21i – 2 + 14i^2 + 42i
z1 – z2 = 4 – 6 – 21i – 2 – 14 + 42i
z1 – z2 = -18 + 21i
Multiplication of Complex Numbers
Let’s first understand the multiplication of two complex numbers (a +bi) and (c+ di).
(a+bi)(c+di)=ac+adi+cbi+bdi2
(a+bi)(c+di)=ac+adi+cbi-bd
The multiplication process of two complex numbers is shown below:
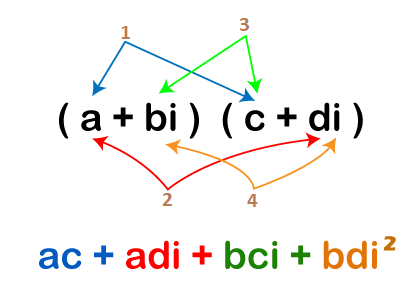
Let the two complex numbers be z1 and z2, where:
z1 = a1 + ib1
z2 = a2 +ib2
The multiplication of two complex number z1 and z2 is denoted as z1z2.
z1z2 = (a1 + ib1)(a2 + ib2)
z1z2=a1a2+a1b2i+a2b1i+b1b2i2
z1z2=a1a2+a1b2i+a2b1i-b1b2
Separating the real and imaginary parts,
z1z2=(a1a2-b1b2)+i(a1b2+a2b1)
We can write the above equation as:
z1z2 = [Re (z1) Re (z2) – Im (z1) Im (z2)] + i[Re (z1) Im (z2) + Re (z2) Im (z1)]
Let’s understand with the help of few examples.
Example 1: If z1 = 3 + 4i and z2 =6 + 7i. Find z1z2.
z1z2 = (3 + 4i) (6 + 7i)
z1z2 = 18 + 21i + 24i + 28i^2
z1z2 = 18 + 21i + 24i – 28
z1z2 = -10 + 45i
Example 2: If z1 = 3 – 4 (i + 4) and z2 =6 – 2i. Find z1z2.
z1z2 = (3 – 4 (i + 4)) (6 – 2i)
z1z2 = (3 – 4i -16) (6 – 2i)
z1z2 = (-13 – 4i) (6 – 2i)
z1z2 = -78 + 26i -24i + 8i^2
z1z2 = -78 + 26i -24i – 8
z1z2 = – -86 + 2i
Division of Complex Numbers
Let the complex number be z = a + ib. The division of a complex number z by a non-zero complex number z1 can be represented as z/z1.
We can also multiply z with the multiplicative inverse of z1. It can also be represented as z/z1.
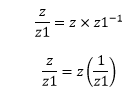
Let z = a + ib and z1 = a1 + ib1.
We can write it as:
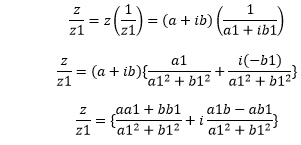
Let’s consider an example.
Example 1: If z1 = 2 + 4i and z2 = 1 + 2i, Find z1/z2.
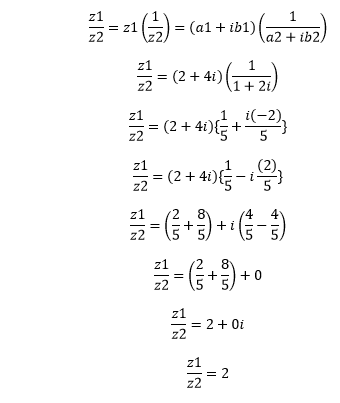
Conjugate of Complex Numbers
Let the complex number be z = a + bi.
Conjugate of a complex number z is a – bi.
Similarly, the conjugate of a complex number 2 + 4i is 2 – 4i.
Hence, the conjugate is defined as the number obtained by replacing the i by -i.
Modulus of a Complex Number
The modulus of a complex number z is denoted by |z|.
It is defined as:
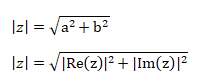
Let’s consider some examples.
Example 1: Find the modulus of z = 3 – 4i.
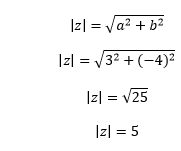
Example 2: Find the modulus of z = 5 + i (6 -3i).
We can write the above complex number as:
z = 5 + 6i + 3
i2=-1
z = 8 + 6i
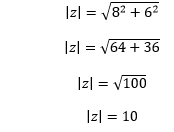
Reciprocal of a Complex Number
Let z = a + ib
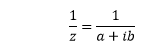
We will multiply the denominator and numerator of a given complex number with its conjugate, as shown below:
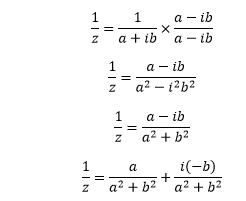
Hence, the multiplication inverse of complex number z is 1/z.
We can say that the multiplicative inverse of a non-zero complex number z is same as it’s reciprocal. It is given by:
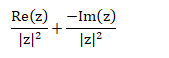
It means conjugate of a complex number divide by the square of its modulus.
Let’s consider some examples.
Example 1: Find the reciprocal of a complex number 2 + 3i.
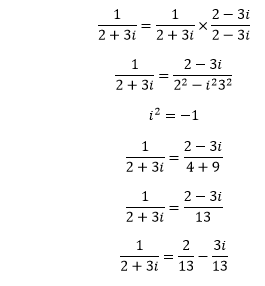
Thus, the reciprocal of the given complex number is:
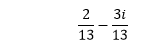
We can also calculate the value directly using the formula:
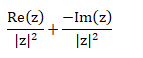
Where,
|z| = 13
Example 2: Find the reciprocal of 5 – 2i.
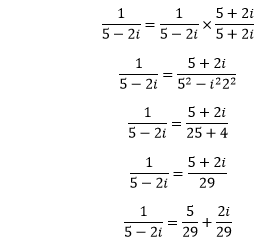
Thus, the reciprocal of the given complex number is:
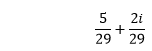
Polar form of a complex number
Let z be the complex number, where z = x +iy. It is represented by a point P (x, y) in the plane, as shown below:
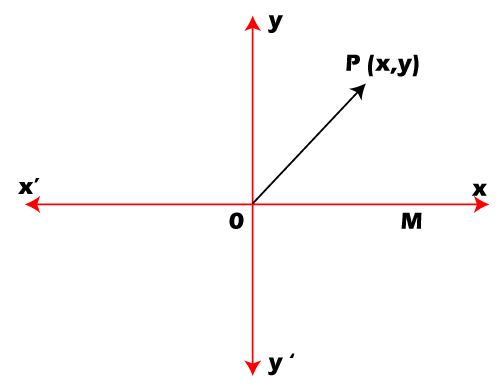
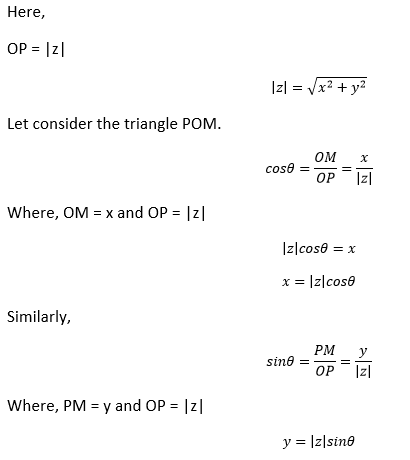
We know, z = x + iy.
Putting the value of x and y in the above equation, we get:
z=|z|cosθ+|z|isinθ
z=|z|(cosθ+isinθ)
We can write it as:
z=r(cosθ+isinθ)
Where,
r=|z|
Such a form of z is known as polar form. Thus, the polar form of z is given by
z=r[cos(2πn+θ)+isin(2πn+θ)]
Where,
r=|z|
n = integer
θ=arg(z)
The arg (z) signifies the angle measured in counter clockwise direction. It depends on the point that lies in one of the four quadrants.
The four quadrants are shown below:
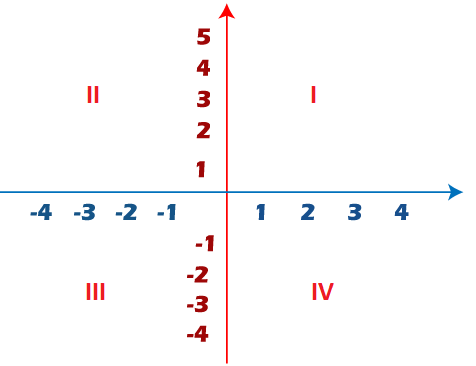
Let,
anglefordifferentqudrants=α
For a point lying in the first quadrant,
θ=α
For a point lying in the second quadrant,
θ=π-α
For a point lying in the third quadrant,
θ=-(π-α)
For a point lying in the fourth quadrant,
θ=-α
Let’s consider some examples.
Example 1: Write the complex number 1 + i in the polar form.
The polar form of a complex number is given by
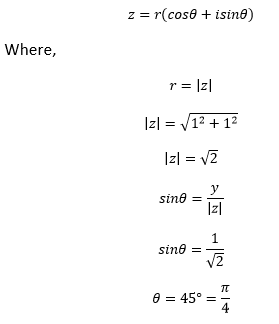
The x and y of the given complex number (1 + i) is (1, 1).
It means that the point (1, 1) lies in the first quadrant.
The arg (z) for the first quadrant is:
θ=α
The polar form of the given complex number is:
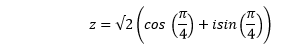
Example 2: Write the complex number -1 – i in the complex form.
The polar form of a complex number is given by
z=r(cosθ+isinθ)
Where,
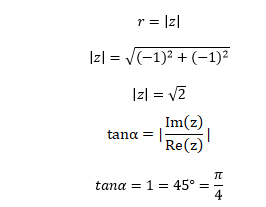
The x and y of the given complex number (1 + i) is (-1, -1).
It means that the point (1, 1) lies in the third quadrant.
The arg (z) for the third quadrant is:
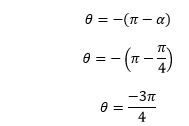
The polar form of the given complex number is:
z=√2
cos(-θ)=cos(θ)∧sin(-θ)=-sin(θ)
Hence, the above polar form can be written as:
z=√2
Example 3: Write the complex number 1 – i in the complex form.
The polar form of a complex number is given by
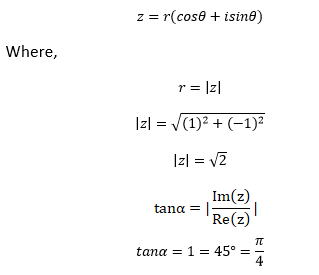
The x and y of the given complex number (1 + i) is (1, -1).
It means that the point (1, 1) lies in the fourth quadrant.
The arg (z) for the fourth quadrant is:
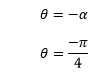
The polar form of the given complex number is:
z=√2
cos(-θ)=cos(θ)∧sin(-θ)=-sin(θ)
Hence, the above polar form can be written as:
z=√2
Square root of a complex number
Let a + ib be a complex number.
√a+ib=x+iy
Where, x and y are the real numbers.
The above equation can be evaluated as:
√a+ib=x+iy
Squaring both sides, we get:
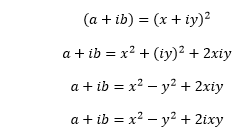
After equation imaginary and real parts, we get:
a=x2-y2
b=2xy
We can write the above equation as:
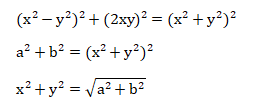
Let’s consider few more examples.
Example 1: Find the square root of the complex number 7 – 24i.
Let us assume,
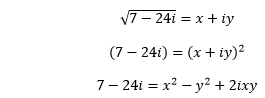
Now, comparing the real and imaginary values, we get:
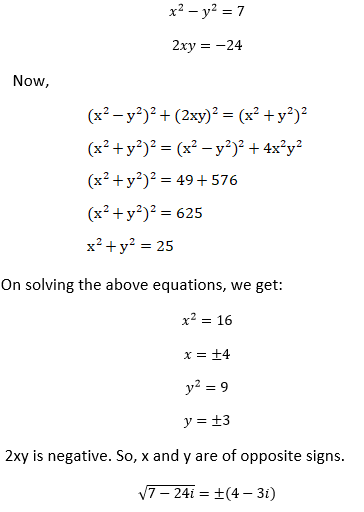
Example 2: Find the square root of the complex number -15 – 8i.
Let us assume,
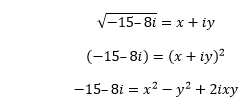
Now, comparing the real and imaginary values, we get: