Recamans Sequence

by Online Tutorials Library July 14, 2022

Recaman’s Sequence

Recamán’s sequence recurrence relation in mathematics and computer science. Because its elements are clearly related to the previous elements, they are frequently defined using recursion.

Definition

The Recamán’s sequence a₀, a₁, a₂ is defined as:

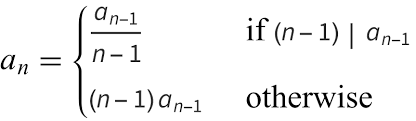
The first terms of the sequence are:

0, 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, 10, 23, 9, 24, 8, 25, 43, 62, 42, 63, 41, 18, 42, 17, 43, 16, 44, 15, 45, 14, 46, 79, 113, 78, 114, 77, 39, 78, 38, 79, 37, 80, 36, 81, 35, 82, 34, 83, 33, 84, 32, 85, 31, 86, 30, 87, 29, 88, 28, 89, 27, 90, 26, 91, 157, 224, 156, 225, 155, …

Print the first n elements of Recaman’s sequence given an integer n.

Examples:

  Input : n = 6  Output : 0, 1, 3, 6, 2, 7    Input  : n = 17  Output : 0, 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, 10, 23, 9, 24, 8  

It is essentially a function with domain and co-domain as natural numbers and 0 respectively. It is defined recursively as follows:

Make a(n) to denote the (n+1)-th term. (0 is already present).

According to Rules:

  a(0) = 0,  if n > 0 and the number is not      already included in the sequence,       a(n) = a(n – 1) – n   else        a(n) = a(n-1) + n.   

A simple implementation is shown below, in which we store all n Recaman Sequence numbers in an array. Using the recursive formula mentioned above, we compute the next number.

C++

  // C++ program to print n-th number in Recaman’s  // sequence  #include   using namespace std;    // Prints first n terms of Recaman sequence  int recaman(int n)  {  // Create an array to store terms  int arr[n];    // First term of the sequence is always 0  arr[0] = 0;  printf(“%d, “, arr[0]);    // Fill remaining terms using recursive  // formula.  for (int i=1; i< n; i++)  {  int curr = arr[i-1] – i;  int j;  for (j = 0; j < i; j++)  {  // If arr[i-1] – i is negative or  // already exists.  if ((arr[j] == curr) || curr < 0)  {  curr = arr[i-1] + i;  break;  }  }    arr[i] = curr;  printf(“%d, “, arr[i]);  }  }    // Driver code  int main()  {  int n = 17;  recaman(n);  return 0;  }  

Output

0, 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, 10, 23, 9, 24, 8,

Time Complexity : O (n²)
Auxiliary Space : O (n)

Optimizations : We can use hashing to store previously computed values, allowing us to run this programme in O(n) time.

C++

  // C++ program to print n-th number in Recaman’s  // sequence  #include   using namespace std;    // Prints first n terms of Recaman sequence  void recaman(int n)  {  if (n <= 0)  return;    // Print first term and store it in a hash  printf(“%d, “, 0);  unordered_set s;  s.insert(0);    // Print remaining terms using recursive  // formula.  int prev = 0;  for (int i=1; i< n; i++)  {  int curr = prev – i;    // If arr[i-1] – i is negative or  // already exists.  if (curr < 0 || s.find(curr) != s.end())  curr = prev + i;    s.insert(curr);    printf(“%d, “, curr);  prev = curr;  }  }    // Driver code  int main()  {  int n = 17;  recaman(n);  return 0;  }  

Output

0, 1, 3, 6, 2, 7, 13, 20, 12, 21, 11, 22, 10, 23, 9, 24, 8,

Time Complexity : O(n)
Auxiliary Space : O(n)

Uses

Recamán’s sequence, in addition to its mathematical and aesthetic properties, can be used to encrypt 2D images using steganography.

Next Topic#

Recamans Sequence

Recaman’s Sequence

Definition

C++

C++

Uses

Accordion CSS

DHTML Tutorial

You may also like