Subarray with given sum

In this problem, we are provided with an unsorted array of non-negative integers and a sum integer value.
We need to find the part from the array, or can we need to find the Subarray, in which the sum of the elements of that array is exactly matched to the given sum.
We need to apply the algorithm to solve this problem, which ultimately results in the desired output.

Let us try to understand it with the help of an example –

We are given an array and a sum.

Example 1 :

Given:

arr = { 10 , 12 , 2 , 4 , 13 , 19 , 5 }

sum = 18

Output :

The given sum is found from indexes 1 to 3

And the subarray is: { 12 , 2 , 4 }

Required sum between indexes of corresponding elements are : 12 + 2 + 4 = 18

Example 2 :

Given:

arr = { 1 , 12 , 2 , 14 , 3 , 16 , 4 }

sum = 19

Output :

The given sum is found from indexes 4 to 5

And the Subarray is: { 3, 16 }

Required sum between indexes of corresponding elements are : 3 + 16 = 19

Example 3 :

Given:

arr = { 1 , 12 , 2 , 14 , 3 , 16 , 4 }

sum = 5

Output :

The given sum is not found in the given array

Example 4 :

Given:

arr = { 1 , 13 , 2 , 14 , 3 , 7 , 4 }

sum = 14

Output :

The given sum is found from indexes 0 to 1

And the Subarray is: { 1, 13 }

Required sum between indexes of corresponding elements are : 1 + 13 = 14

Here if we observe that, we have more than one Subarray, in which the sum of all elements is equal to 14, i.e., are as follows –

First subarray is found from indexes 0 to 1, i.e., { 1 , 13 }.
Second subarray is found on index 3, i.e., { 14 }.
The third Subarray is found from indexes 4 to 6, i.e., { 3, 7, 4 }.

What is the output if we get multiple such sub-arrays producing the desired sum by adding their elements?

It will display the first shortest Subarray, whose sum of elements exactly matches the given sum. We are deriving the algorithm based on the above logic; in short, we are finding the sub-array that matches the corresponding given sum at the very first time.

Methods to Solve the Problem for finding the Subarray from the given array, whose sum of elements matches with the given sum –

To use the Brute force approach, an inefficient and simple method.
To use the Linear complexity method, an efficient approach.

Let us find the Subarray from the given array, whose sum matches the given sum using these methods mentioned above.

Method # 1 Brute Force approach, an inefficient and simple method –

The method a programmer must prefer is always brute force approach, which will increase our understanding of the problem. Once we have solved this problem using this method, it will lead to raising our confidence level, and after then we can go further to try with the other methods, which is probably more efficient then this method.

Let us discuss the above problem using this method:

As we have already seen, the working of this problem, we all need to find a subarray in which the sum of all elements matches with the given sum value.

Algorithm to implement Brute force approach to solve this problem –

Step 1 – Take an array from the user of ‘ n ‘ elements; which refer to the non-negative integers in the main function. We can also take the sum value from the user to generate the result accordingly.

Step 2 – Make a function call to find a subarray in which the sum of all the elements matches the given sum. Pass the original array, number of elements, and given sum value in the function as an argument.

Step 3 – In a Subarray function, run two loops; one loop will run from the 0^th index of the array to the last index. We can define i = 0 to i = n-1 to traverse the array from index 0 to the last index.

Step 4 – Another loop is inside the first loop, as we can say nested loop, and it will run from j = i + 1 to n.

Step 5 – At the starting of this subarray function, declare a variable named currentsum; which will initially be initialized with arr [ 0 ].

Step 6 – In the second loop, derive the condition to check whether the current sum is equal to the given sum or not; if it equals, then print the result in the form of indexes.

Step 7 – If not, check if the currentsum is greater than the sum of j == n or not; if this condition is true, break from the loop.

Step 8 – Finally assign currentsum = currentsum + arr [ j ].

Step 9 – Step 8 will calculate the current sum by incrementing the value of currentsum by adding the value present at index j if the conditions of currentsum == sum fail.

Step 10 – After executing loop1 and nested loop2 inside loop1, we will get the desired result.

Step 11 – If a still case arises where the currentsum does not match the given sum, it indicates that no such subarray exists in the main array.

Step 12 – Finally, we will get the desired output, as a result, on the screen.

Implementation of Subarray with given sum Problem using Method # 1 in C Programming Language

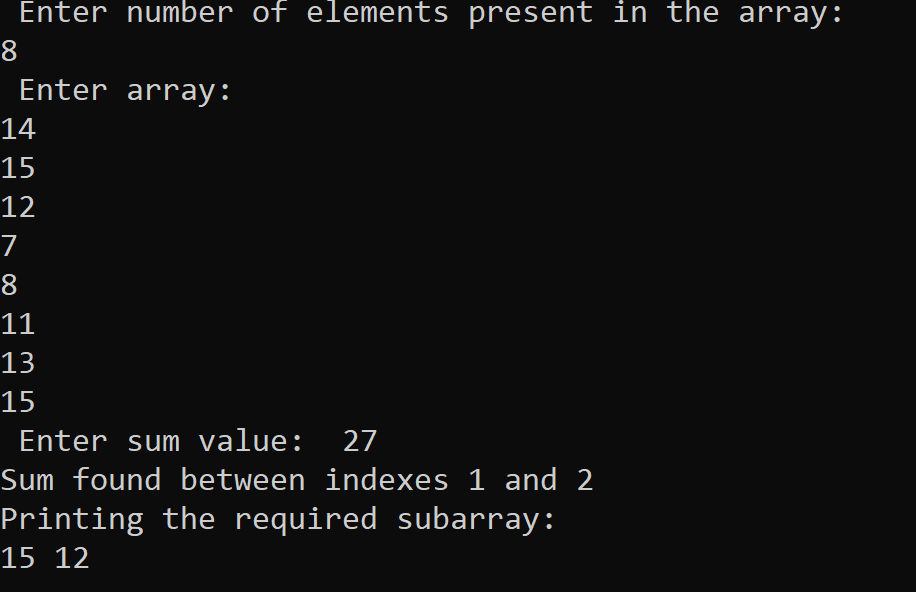
  /* C program to print Subarray with given sum using Brute force approach */  #include   /* The program will print the indexes if the currentsum is equal to the sum, else it will print sum will not found */  int  subarray ( int arr[], int n, int sum )  {  int currentsum, i , j , k ;  // Start with initial index 0 element  for ( i = 0 ; i < n ; i++ )   {  currentsum = arr[ i ] ;  // try all subarrays starting with ‘i’  for ( j = i + 1 ; j <= n ; j++ )   {  if (currentsum == sum) {  printf ( ” Sum found between indexes %d and %dn ” , i , j -1 ) ;  printf( ” Printing the required subarray: n ” ) ;  for( k = i ; k <= j – 1 ; k++ )  {  printf( ”  %d “,arr[ k ] ) ;  }                                                 return 0 ;  }  if ( currentsum > sum || j == n )  break ;  currentsum = currentsum + arr[ j ] ;  }  }    printf( ” n No subarray found n ” ) ;  }  int main()  {  int i , A[ 100 ] , n , sum ;  printf ( ” Enter number of elements present in the array : ” ) ;  scanf ( “%d ” , &n ) ;  printf( ” Enter array: ” ) ;  for ( i = 0 ;  i < n ; i++ )  {  scanf ( “%d ” , &A[ i ] ) ;  }  printf( ” Enter sum value: ” ) ;  scanf( “%d ” , ∑ ) ;  subarray ( A , n , sum ) ;  return 0 ;  }  

The output of the following C program for solving the Subarray with given sum problem using Method # 1

subarray with given sum

Implementation of Subarray with given sum Problem using Method # 1 in C++ Programming Language

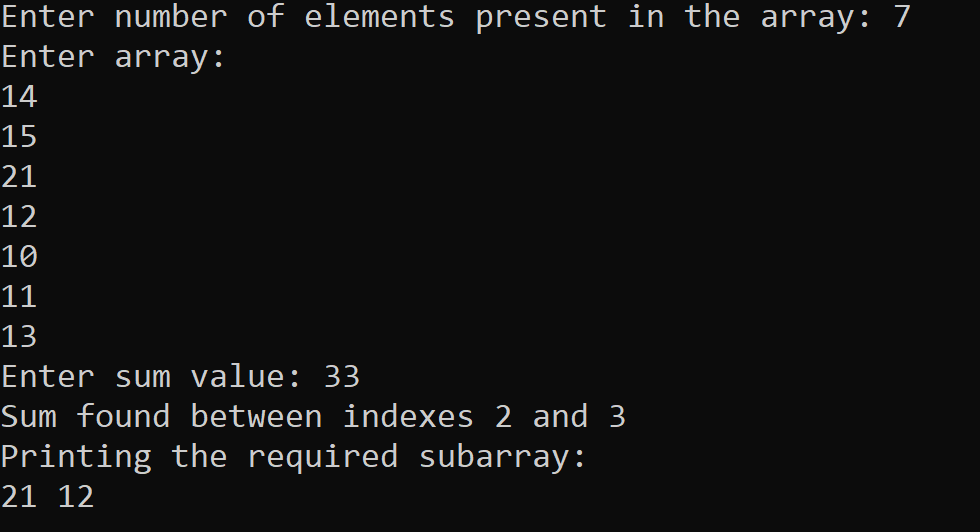
  /* C++ program to print subarray with given sum using Brute force approach */  #include   using namespace std;  /* The program will print the indexes if the currentsum is equal to the sum, else it will print sum will not found */  int subarray ( int arr[] , int n , int sum )  {  int currentsum, i, j, k ;    // Start with initial index 0 element  for ( i = 0 ; i < n ; i++ )   {  currentsum = arr[ i ] ;    // try all subarrays starting with ‘ i ‘  for ( j = i + 1 ; j <= n ; j++ )   {  if ( currentsum == sum )   {  cout<<  ” Sum found between indexes  ” <<  i << ” and ” <<  j – 1 << endl ;  cout << ” Printing the required subarray : ” << endl ;  for( k = i ; k <= j-1 ; k++ )  {  cout << arr[ k ] << ” ” ;  }  return 0 ;  }  if ( currentsum  >  sum || j == n )  break ;  currentsum = currentsum + arr[ j ] ;  }    }  cout << endl ;  cout  << ” No subarray found ” << endl ;  }    int main()  {  int i ,  A[ 100 ] , n , sum ;  cout << ” Enter number of elements present in the array : ” << endl ;  cin >> n ;  cout << ” Enter array :  ” << endl ;  for ( i = 0 ; i < n ; i++ )  {  cin >> A [ i ] ;   }  cout << ” Enter sum value:  ” ;  cin >> sum ;  subarray ( A , n , sum ) ;    return 0 ;  }  

The output of the following C++ program for solving the Subarray with given sum problem using Method # 1

subarray with given sum

Implementation of Subarray with given sum Problem using Method # 1 in Python Programming Language

  # Python program to print Subarray with given sum using Brute force approach   # The program will print the indexes if the currentsum is equal to the sum; else, it will print sum will not be found     def subarray(A,n,sum):    for i in range(n):          currentsum = A[i]          # start array with the initial index           # try all subarrays          # starting with ‘i’          j = i + 1          while j <= n:                         if currentsum == sum:                  print(“Sum found between”)                  print(“indexes % d and % d”%( i, j-1))                                     return 1                                 if currentsum > sum or j == n:                  break                             currentsum = currentsum + A[j]              j = j + 1          print(“No subarray found”)          return 0    print(“Enter size of an array: “)  n=int(input())  print(“Enter array elements: “)  i=0  A=[]  while(i):>

The output of the following Python program for solving the Subarray with given sum problem using Method # 1

subarray with given sum

Implementation of Subarray with given sum Problem using Method # 1 in Java Programming Language

  // Java program to print Subarray with given sum using Brute force approach   // The program will print the indexes if the currentsum is equal to the sum; else, it will print sum will not be found     import java.util.Scanner ;    class Main {  /* If our function subarray seems to be successful in finding any subarray whose sum of elements matches with the given sum value, then we will print the resulting Subarray, else we will return -1./  static int subarray(int arr[] , int n , int sum )  {  int currentsum, i , j ;  // start array with the initial index try all subarrays starting with  ‘ i ‘    for ( i = 0 ; i < n ; i++ ) {  currentsum = arr[ i ] ;  for (j = i + 1 ; j <= n ; j++) {  if (currentsum == sum) {  int p = j – 1 ;  System.out.println(  ” Sum found between indexes  ” + i  + ” and ” + p) ;  return 1 ;  }  if (currentsum > sum || j == n)  break ;  currentsum = currentsum + arr[j] ;  }  }    System.out.println(” No subarray found ” ) ;  return 0 ;  }    public static void main( String[] args )  {  int n ;   Scanner sc = new Scanner ( System.in ) ;    System.out.println ( ” Enter number of elements :  ” ) ;   n = sc.nextInt() ;   int [] array = new int[ 100 ] ;   System.out.println ( ” Enter elements of the array :  ” ) ;   for ( int i = 0 ; i < n ; i++ )   {   array[ i ] = sc.nextInt() ;   }   System.out.println( ” Enter value of sum : ” ) ;   int sum = sc.nextInt() ;   subarray( array , n , sum ) ;  }  }  

The output of the following Java program for solving the Subarray with given sum problem using Method # 1

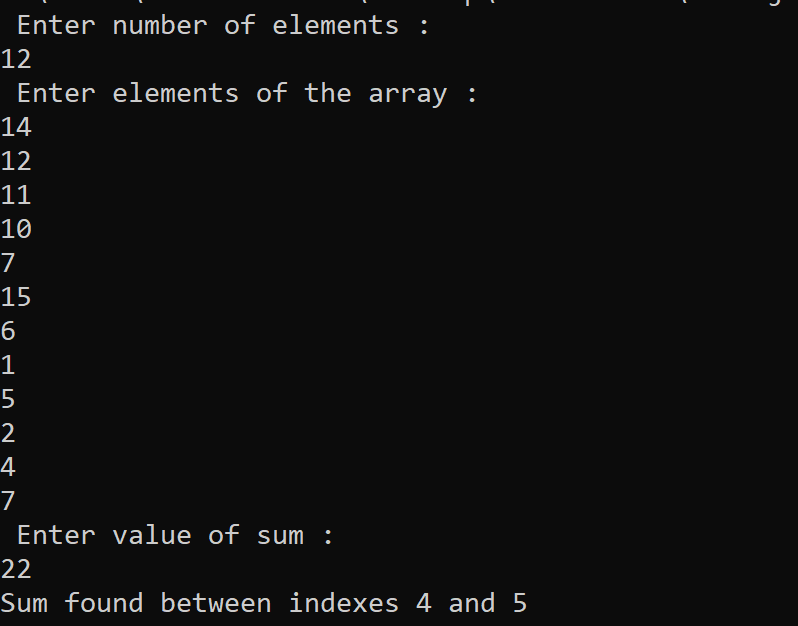
subarray with given sum

Implementation of Subarray with given sum Problem using Method # 1 in C# Programming Language

  // C# program to print Subarray with given sum using Brute force approach   // The program will print the indexes if the currentsum is equal to the sum; else, it will print sum will not be found     using System ;  class Main {  /* If our function subarray seems to be successful in finding any subarray whose sum of elements matches with the given sum value, then we will print the resulting Subarray, else we will return -1./    int subarray( int[] arr, int n , int sum )  {  int currentsum , i, j ;             // start array with the initial index           //  try all subarrays starting with  ‘ i ‘    for (i = 0 ; i < n ; i++) {  currentsum = arr[i] ;  for (j = i + 1 ; j <= n ; j++) {  if (currentsum == sum) {  int p = j – 1 ;  Console.Write(“Sum found between ”  + “indexes ” + i + ” and ” + p) ;  return 1 ;  }  if (currentsum > sum || j == n)  break ;  currentsum = currentsum + arr[j] ;  }  }    Console.Write(“No subarray found”) ;  return 0 ;  }  public static void Main()  {  Main arraysum = new Main();  int[] arr = { 1, 2, 4, 5, 9, 10, 14, 23 };  int n = arr.Length;  int sum = 11;  arraysum.subarray(arr, n, sum);  }  }  

The output of the following C# program for solving the Subarray with given sum problem using Method # 1

subarray with given sum

After executing the program successfully in a specific programming language and following the Brute force algorithm using the double traversal approach, we will get the proper result, i.e., finding the resultant Subarray, whose sum of elements is exactly equal to the given sum value.

Now let us analyze the running time and performance of the algorithm we are applying to sort the array in ascending order by finding the algorithm’s time complexity and space complexity using in Method # 1.

Time Complexity of Method # 1 –

For finding the time complexity, we need to observe the algorithm and analyze the time taken by a particular line for execution. We can observe that we require traversing the array using two for loops and checking the condition for finding the sum. Hence time complexity will be –

T ( n ) = O ( n ).O ( n )

T ( n ) = O ( n² )

Hence time complexity will be O ( n² ), as we do the asymptotically rough idea that we require ‘ n² ‘ time to solve the problem of ‘ n ‘ elements.

Space Complexity of Method # 1 –

To find space complexity, we need to observe the program and analyze the space required to store all the variables; as we notice the program, we will observe that no extra space is required to store the elements.

S ( n ) = O ( 1 )

Hence the space complexity for above method # 1 will be constant.

Method # 2 Linear Complexity method, an inefficient and simple approach –

As we have already seen the working of method 1, i.e., Brute force approach, we will move further towards a more efficient method; it is very easy to implement to solve any problem; as the name suggests, the linear complexity method has linear complexity. Once you have succeeded in making the program, try to find the other best alternative to solve the given problem, in a much more efficient way, whose performance is better and time complexity is less than this method.

Let us discuss the above problem using this method:

As we have already seen, the working of this problem, we all need to find a subarray in which the sum of all elements matches with the given sum value.

Algorithm to implement Linear complexity method to solve this problem –

Step 1 – Take an array from the user of ‘ n ‘ elements; elements refer to the non-negative integers in the main function. Also, take the sum value from the user so that we can generate the result accordingly.

Step 3 – In a Subarray function, run one loop only; it will run from the 0^th index of the array to the last index. We can define i = 0 to i = n-1 to traverse the array from index 0 to the last index. Also, assign a variable named ‘ begin ‘ with 0.

Step 4 – At the starting of this subarray function, declare a variable named currentsum; this variable will initially be initialized with arr [ 0 ].

Step 5 – Inside that loop, we will run a while loop to check the condition whether the currentsum is greater than the given sum, and begin is less than i – 1; if this condition is true, then we will update the current sum variable as current sum – arr [ begin ], after then increment begin as begin = begin + 1.

Step 6 – After that, out from the while loop, check the condition using if statement as, whether currentsum equals sum or not.

Step 7 – If true, print the result as the sum between the indexes, begin, and i – 1.

Step 8 – After then check one more statement using the if statement, whether i is less than n or not.

Step 9 – If proved true, update the currentsum with currentsum + arr [ i ].

Step 10 – If a still case arises where the currentsum does not match the given sum, it indicates that no such subarray exists in the main array.

Step 11 – Finally, we will get the desired output, as a result, on the screen.

Implementation of Subarray with given sum Problem using Method # 2 in C Programming Language

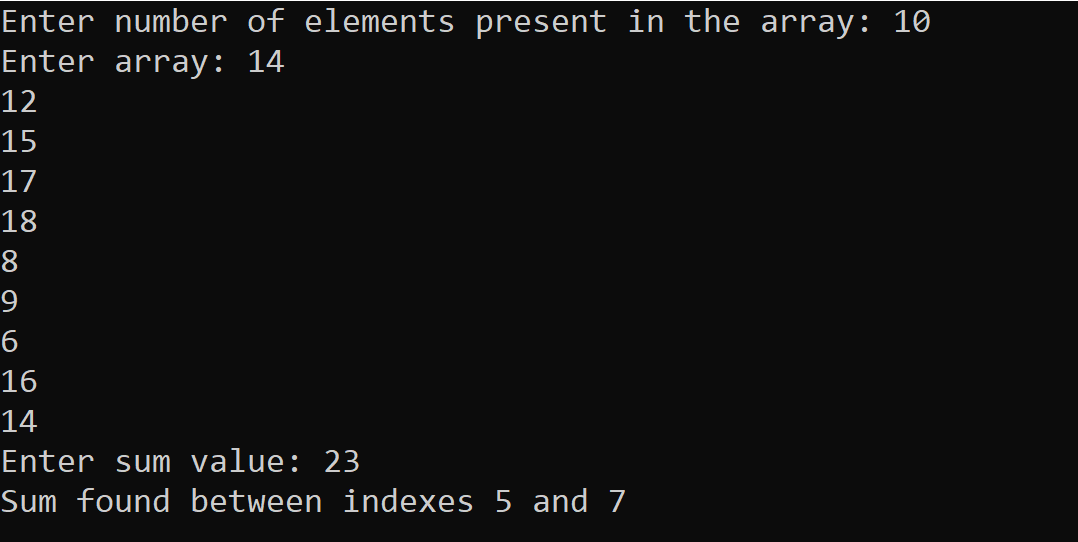
  /* C program to print subarray with given sum using Linear complexity method */  #include   /* The program will print the indexes if the currentsum is equal to the sum, else it will print sum will not found */  int subarray ( int arr[] , int n , int sum )  {  int currentsum = arr [ 0 ] , begin = 0 , i ;         /* Add elements one by one to  currentsum and if the currentsum         exceeds the sum, then remove  starting element */      for ( i = 1 ; i <= n ; i++ )   {          // If currentsum exceeds the sum ,          // then remove the starting elements          while (currentsum > sum && begin < i – 1 ) {              currentsum = currentsum – arr[ begin ] ;              begin++ ;          }             // If currentsum becomes equal to sum,          // then return true          if ( currentsum == sum ) {              printf(                  ” Sum found between indexes %d and %d ” ,                  Begin , i – 1) ;              return 1 ;          }             // Add this element to currentsum          if ( i < n)              currentsum = currentsum + arr [ i ] ;      }         // If we reach here, then no subarray      printf ( ” No subarray found”) ;      return 0 ;   }    int main()  {  int i , A[ 100 ] , n , sum ;  printf ( ” Enter number of elements present in the array : ” ) ;  scanf ( “%d ” , &n ) ;  printf ( ” Enter array : ” ) ;  for( i = 0 ; i < n ; i++ )  {  scanf (“%d ” , &A[ i ] ) ;  }  printf ( ” Enter sum value : ” ) ;  scanf (“%d ” , ∑ ) ;  subarray ( A , n , sum ) ;  return 0 ;  }  

The output of the following C program for solving the Subarray with given sum problem using Method # 2

subarray with given sum

Implementation of Subarray with given sum Problem using Method # 2 in C++ Programming Language

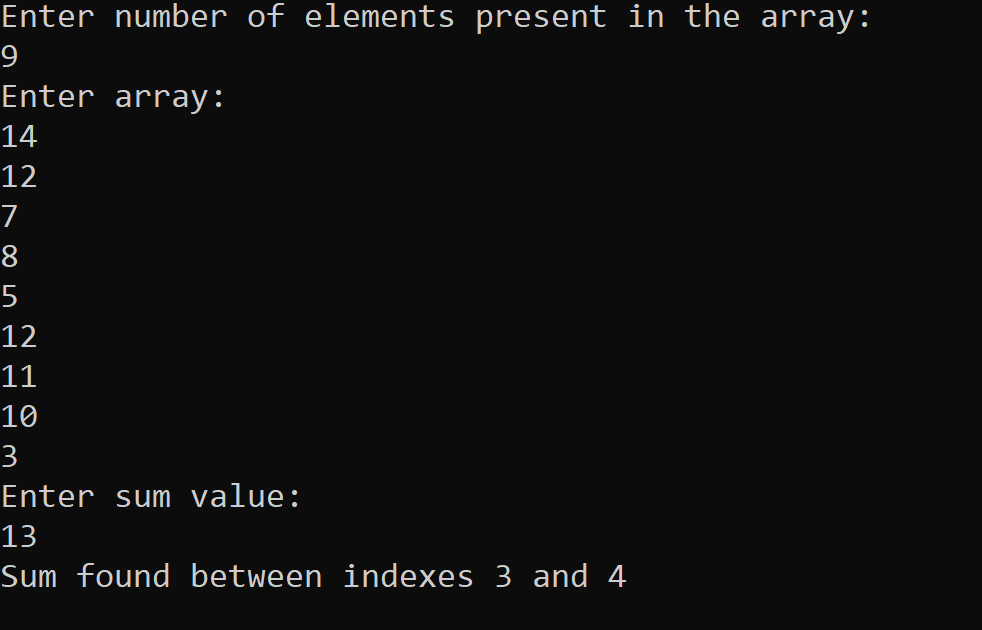
  /* C++ program to print subarray with given sum using Linear complexity method */  #include   using namespace std ;  /* The program will print the indexes if the currentsum is equal to the sum, else it will print sum will not found */  int subarray(int arr[] , int n , int sum )  {  int currentsum = arr[ 0 ] , begin = 0 , i ;         /* Add elements one by one to  currentsum and if the currentsum         exceeds the sum , then remove  starting element */      for ( i = 1 ; i <= n ; i++) {          // If currentsum exceeds the sum ,          // then remove the starting elements          while ( currentsum > sum && begin < i – 1) {              currentsum = currentsum – arr[ begin ] ;              begin++ ;          }             // If currentsum becomes equal to sum,          // then return true          if ( currentsum == sum ) {              cout<<” Sum found between indexes ” << begin << ” and ” << i – 1 << endl ;              return 1 ;          }          // Add this element to currentsum          if (i < n)              currentsum = currentsum + arr[ i ] ;      }         // If we reach here, then no subarray      cout << ” No subarray found ” << endl ;      return 0 ;  }    int main()  {  int i , A[ 100 ] ,n , sum ;  cout << ” Enter number of elements present in the array : ” << endl ;  cin >> n ;  cout << ” Enter array : ” << endl ;  for ( i = 0 ; i < n ; i++ )  {  cin >> A[ i ] ;  }  cout << ” Enter sum value : ” << endl ;  cin >> sum ;  subarray ( A , n , sum ) ;    return 0 ;  }  

The output of the following C++ program for solving the Subarray with given sum problem using Method # 2

subarray with given sum

Implementation of Subarray with given sum Problem using Method # 2 in Java Programming Language

  /* Java program to print Subarray with given sum using Linear complexity method */  /* The program will print the indexes if the currentsum is equal to the sum, else it will print sum will not found */    import java.util.Scanner ;    class Main {  /* Returns true if the there is a  subarray of arr[] with a sum equal to  ‘sum’ otherwise returns false.  Also, prints the result */  static int subarray(int arr[], int n, int sum)  {  int currentsum = arr[0], begin = 0, i;             // Always start with the initial index of an array          for (i = 1; i <= n; i++) {              // If currentsum exceeds the sum,              // then remove the starting elements              while (currentsum > sum && begin < i – 1) {                  currentsum = currentsum – arr[begin];                  begin++;              }                 // If currentsum becomes equal to sum,              // then return true              if (currentsum == sum) {                  int p = i – 1;                  System.out.println(                      “Sum found between indexes ” + begin                      + ” and ” + p);                  return 1;              }                 // Add this element to currentsum              if (i < n)                  currentsum = currentsum + arr[i];          }             System.out.println(“No subarray found”);          return 0;  }    public static void main(String[] args)  {  int n ;   Scanner sc = new Scanner ( System.in ) ;   System.out.println ( ” Enter number of elements :  ” ) ;   n = sc.nextInt() ;   int [] array = new int[ 100 ] ;   System.out.println ( ” Enter elements of the array :  ” ) ;   for ( int i = 0 ; i < n ; i++ )   {   array[ i ] = sc.nextInt() ;   }   System.out.println( ” Enter value of sum : ” ) ;   int sum = sc.nextInt();   subarray( array , n , sum ) ;  }  }  

The output of the following Java program for solving the Subarray with given sum problem using Method # 2

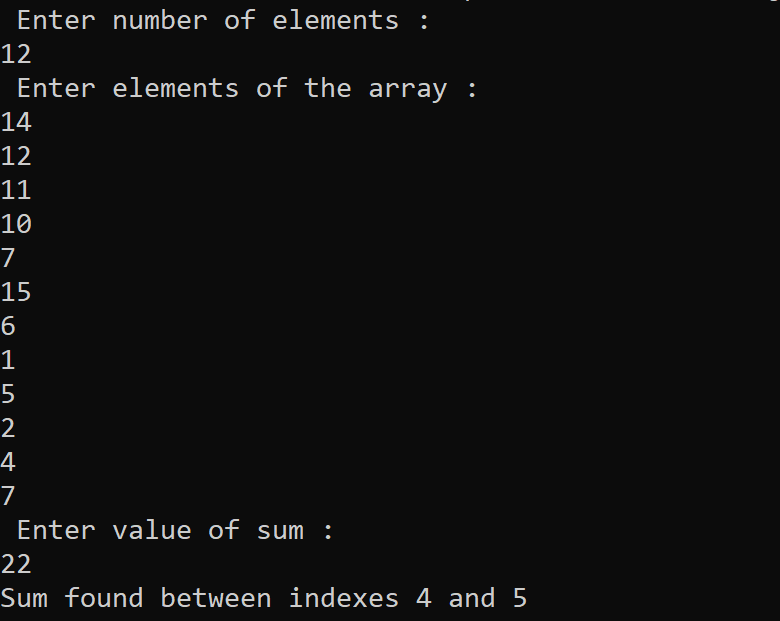
subarray with given sum

Implementation of Subarray with given sum Problem using Method # 2 in Python Programming Language

  # Python program to print Subarray with given sum using Linear complexity method   # The program will print the indexes if the currentsum is equal to the sum; else, it will print sum will not be found     def subarray(arr,n,sum):    currentsum = arr[0]    begin = 0         # Add elements one by      # one to currentsum and      # if the currentsum exceeds      # the sum, then remove      # starting element    i = 1    while i <= n:                     # If currentsum exceeds          # the sum, then remove          # the starting elements        while currentsum > sum and begin < i-1:                       currentsum = currentsum – arr[begin]            begin = begin + 1                         # If currentsum becomes          # equal to sum, then          # return true        if currentsum == sum:            print(“Sum found between indexes”)            print(“% d and % d”%(begin, i-1))            return 1             # Add this element          # to currentsum        if i < n:            currentsum = currentsum + arr[i]        i = i + 1         # If we reach here,      # then no subarray    print(“No subarray found”)    return 0  print(“Enter size of an array: “)  n=int(input())  print(“Enter array elements: “)  i=0  A=[]  while(i):>

The output of the following Python program for solving the Subarray with given sum problem using Method # 2

subarray with given sum

Implementation of Subarray with given sum Problem using Method # 2 in C# Programming Language

  /* C# program to print Subarray with given sum using Linear complexity method */  /* The program will print the indexes if the currentsum is equal to the sum, else it will print sum will not found */  using System ;    class Main {    // Returns true if the  // there is a subarray of  // arr [ ] with sum equal to  // ‘ sum ‘ otherwise returns false.  // Also, prints the result  int subarray( int[] arr , int n , int sum )  {  int currentsum = arr[ 0 ] ,  begin = 0 , i ;  // Always start with an initial index of an array  for ( i = 1 ; i <= n ; i++ ) {  // If currentsum exceeds  // the sum, then remove  // the starting elements  while ( currentsum > sum && begin < i – 1 ) {  currentsum = currentsum – arr[ begin ] ;  begin++ ;  }    // If currentsum becomes equal to  // sum, then return true  if (currentsum == sum) {  int p = i – 1 ;  Console.WriteLine(” Sum found between “+ ” indexes ” + begin + ” and ” + p) ;  return 1 ;  }    // Add this element to currentsum  if (i < n)  currentsum = currentsum + arr[ i ] ;  }  Console.WriteLine( ” No subarray found ” ) ;  return 0 ;  }  public static void main()  {  Main arraysum = new Main() ;  int[] arr = new int[] { 15 , 2 , 19 , 20 , 9 , 5 , 10 } ;  int n = arr.Length ;  int sum = 39 ;  arraysum.subarray( arr , n , sum ) ;  }  }  

The output of the following C# program for solving the Subarray with given sum problem using Method # 2

subarray with given sum

Now let us analyze the performance and running time of the algorithm we are applying to find a subarray in which the sum of its elements is equal to the given sum value by finding the algorithm’s time complexity and space complexity using in Method # 2.

Time Complexity of Method # 2 –

For finding the time complexity, first, we need to observe the algorithm and analyze the time taken by a particular line of code for execution. We can observe that traversing of an array is done by using only one for loop and checking the condition for finding the sum. Hence time complexity will be –

T ( n ) = O ( n ) + C

Here, ‘ C ‘ be any constant

T ( n ) = O ( n )

Hence time complexity will be O ( n ), as we do the asymptotically rough idea that we require ‘ n ‘ time to solve the problem of ‘ n ‘ elements.

Space Complexity of Method # 2 –

To find space complexity, we need to observe the lines of code and analyze the space required to store all the variables, as we notice the program that no extra space is required to store the elements.

S ( n ) = O ( 1 )

Hence the space complexity for above method # 2 will be constant.

Next TopicSelf-organizing List

Subarray with given sum

Subarray with given sum

Example 1 :

Example 2 :

Example 3 :

Example 4 :

What is the output if we get multiple such sub-arrays producing the desired sum by adding their elements?

Methods to Solve the Problem for finding the Subarray from the given array, whose sum of elements matches with the given sum –

Method # 1 Brute Force approach, an inefficient and simple method –

Method # 2 Linear Complexity method, an inefficient and simple approach –

Algorithm to implement Linear complexity method to solve this problem –

Priority Queue using Linked list

Bitmap Indexing

You may also like