Rotation:

It is a process of changing the angle of the object. Rotation can be clockwise or anticlockwise. For rotation, we have to specify the angle of rotation and rotation point. Rotation point is also called a pivot point. It is print about which object is rotated.

Types of Rotation:

Anticlockwise
Counterclockwise

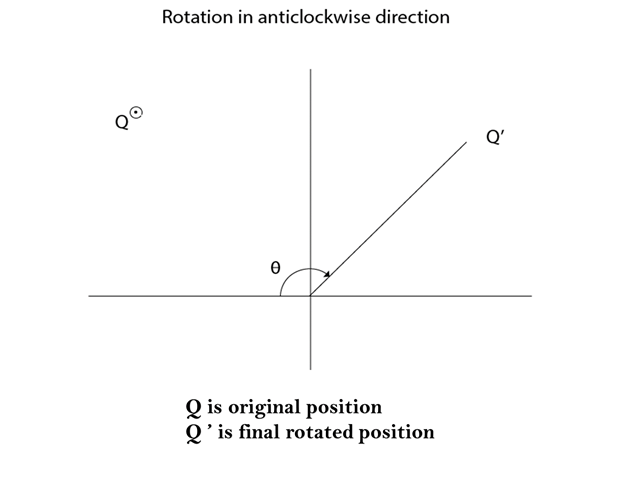
The positive value of the pivot point (rotation angle) rotates an object in a counter-clockwise (anti-clockwise) direction.

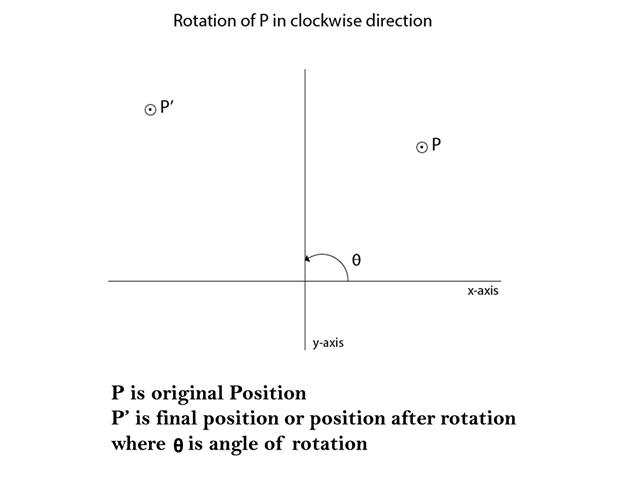
The negative value of the pivot point (rotation angle) rotates an object in a clockwise direction.

When the object is rotated, then every point of the object is rotated by the same angle.

Straight Line: Straight Line is rotated by the endpoints with the same angle and redrawing the line between new endpoints.

Polygon: Polygon is rotated by shifting every vertex using the same rotational angle.

Curved Lines: Curved Lines are rotated by repositioning of all points and drawing of the curve at new positions.

Circle: It can be obtained by center position by the specified angle.

Ellipse: Its rotation can be obtained by rotating major and minor axis of an ellipse by the desired angle.

Matrix for rotation is a clockwise direction.

Matrix for rotation is an anticlockwise direction.

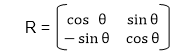
Matrix for homogeneous co-ordinate rotation (clockwise)

Matrix for homogeneous co-ordinate rotation (anticlockwise)

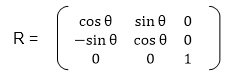
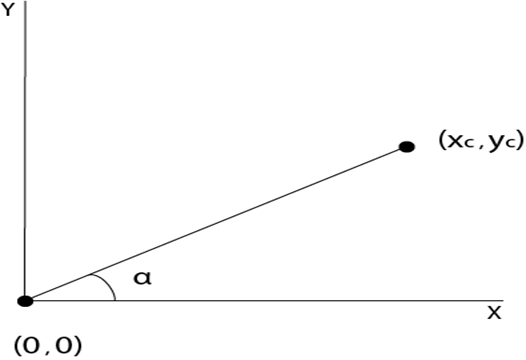
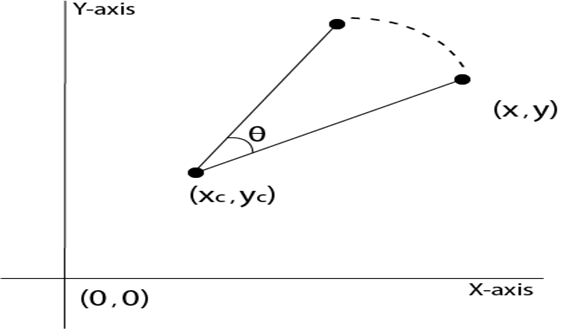
Rotation about an arbitrary point: If we want to rotate an object or point about an arbitrary point, first of all, we translate the point about which we want to rotate to the origin. Then rotate point or object about the origin, and at the end, we again translate it to the original place. We get rotation about an arbitrary point.

Example: The point (x, y) is to be rotated

The (x_c y_c) is a point about which counterclockwise rotation is done

Step1: Translate point (x_c y_c) to origin

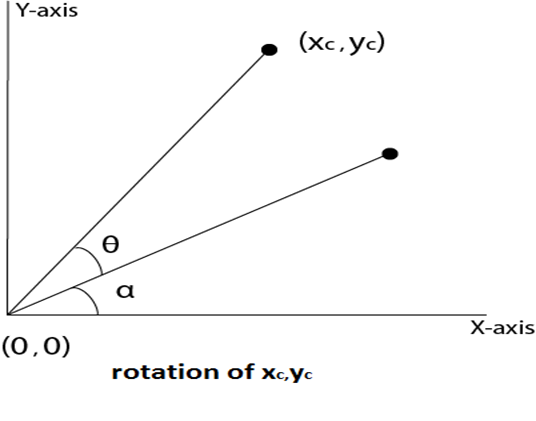
Step2: Rotation of (x, y) about the origin

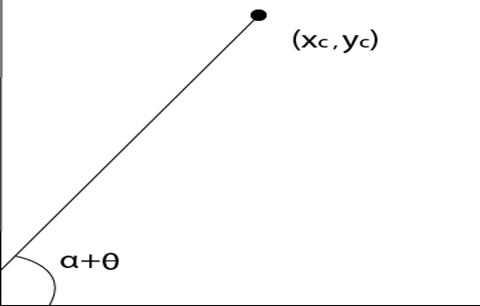
Step3: Translation of center of rotation back to its original position

Example1: Prove that 2D rotations about the origin are commutative i.e. R₁ R₂=R₂ R₁.

Solution: R₁ and R₂are rotation matrices

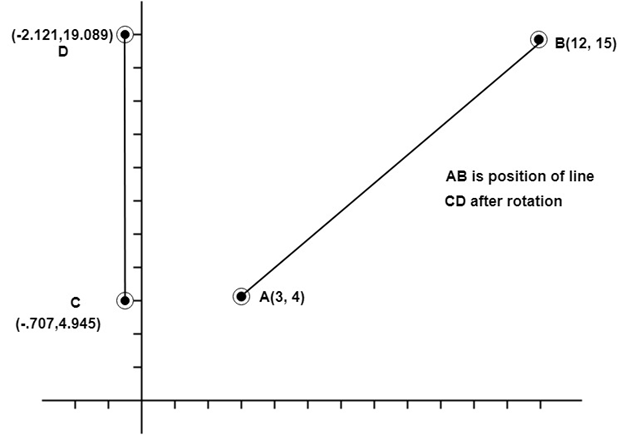
Example2: Rotate a line CD whose endpoints are (3, 4) and (12, 15) about origin through a 45° anticlockwise direction.

Solution: The point C (3, 4)

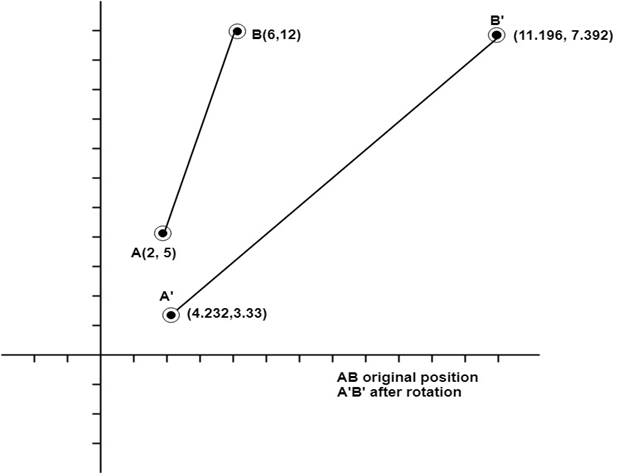
Example3: Rotate line AB whose endpoints are A (2, 5) and B (6, 12) about origin through a 30° clockwise direction.

Solution: For rotation in the clockwise direction. The matrix is

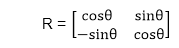
Step1: Rotation of point A (2, 5). Take angle 30°

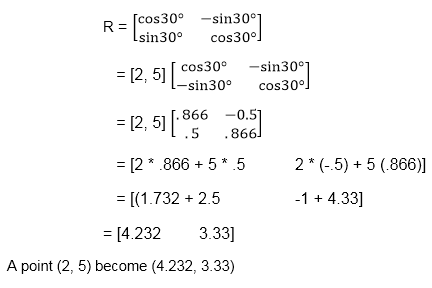
Step2: Rotation of point B (6, 12)

Program to rotate a line:

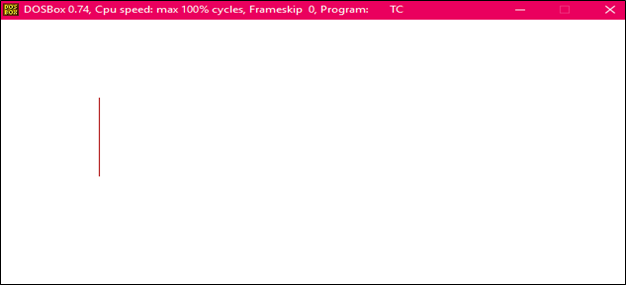
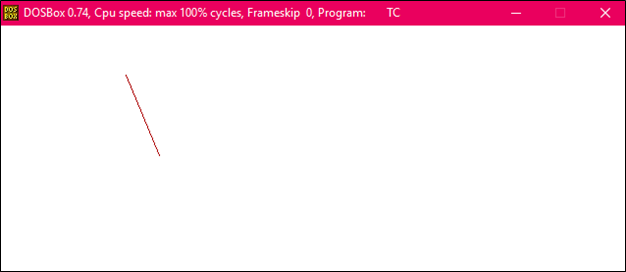
  #include  #include  #include  int main()  {  intgd=0,gm,x1,y1,x2,y2;  double s,c, angle;  initgraph(&gd, &gm, “C:\TC\BGI”);  setcolor(RED);  printf(“Enter coordinates of line: “);  scanf(“%d%d%d%d”,&x1,&y1,&x2,&y2);  cleardevice();  setbkcolor(WHITE);  line(x1,y1,x2,y2);  getch();  setbkcolor(BLACK);  printf(“Enter rotation angle: “);  scanf(“%lf”, ∠);  setbkcolor(WHITE);  c = cos(angle *3.14/180);  s = sin(angle *3.14/180);  x1 = floor(x1 * c + y1 * s);  y1 = floor(-x1 * s + y1 * c);  x2 = floor(x2 * c + y2 * s);  y2 = floor(-x2 * s + y2 * c);  cleardevice();  line(x1, y1 ,x2, y2);  getch();  closegraph();  return 0;  }  

Output:

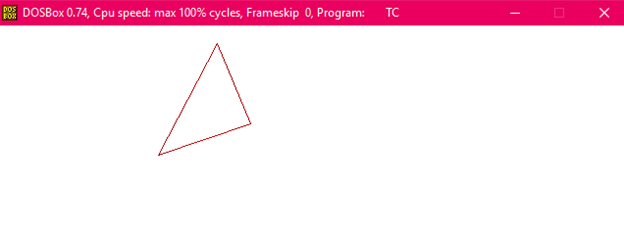
Before rotation

After rotation

Program to rotate a Triangle:

  #include  #include  #include  main()  {  intgd=0,gm,x1,y1,x2,y2,x3,y3;  double s,c, angle;  initgraph(&gd, &gm, “C:\TURBOC3\BGI”);  setcolor(RED);  printf(“Enter coordinates of triangle: “);  scanf(“%d%d%d%d%d%d”,&x1,&y1,&x2,&y2, &x3, &y3);  setbkcolor(WHITE);  cleardevice();  line(x1,y1,x2,y2);  line(x2,y2, x3,y3);  line(x3, y3, x1, y1);  getch();  setbkcolor(BLACK);  printf(“Enter rotation angle: “);  scanf(“%lf”, ∠);  setbkcolor(WHITE);  c = cos(angle *M_PI/180);  s = sin(angle *M_PI/180);  x1 = floor(x1 * c + y1 * s);  y1 = floor(-x1 * s + y1 * c);  x2 = floor(x2 * c + y2 * s);  y2 = floor(-x2 * s + y2 * c);  x3 = floor(x3 * c + y3 * s);  y3 = floor(-x3 * s + y3 * c);  cleardevice();  line(x1, y1 ,x2, y2);  line(x2,y2, x3,y3);  line(x3, y3, x1, y1);  getch();  closegraph();  return 0;  }  

Output:

Before rotation

After rotation

Next TopicReflection

2d transformation 3d computer graphics 3d transformation animation techniques cathode ray tube circle generation algorithm color crt monitors computer animation computer graphics tutorial crt curves display processor flat panel display fractals introduction keyframing line generation algorithm polygon filling algorithm random scan display raster scan display surfaces types of curves viewing and clipping

Computer Graphics Rotation

Rotation:

Types of Rotation:

Program to rotate a line:

Program to rotate a Triangle:

Why is my Internet connection so slow

BGP | Border Gateway Protocol

You may also like