74

C++ Bitwise XOR Operator

• Bitwise XOR operator is also known as Exclusive OR
• It is denoted by using the ‘^’
• As the name depicts, it works on the bit level of the operands.
• Bitwise XOR operator has come under the category of Bitwise operators.
• In the bitwise exclusive OR operator (XOR), two operands are required, and these two operands are separated by the XOR symbol, i.e., ‘^’.
• To determine the output or result that comes out after applying the XOR operator on two operands, we need to follow the Logical truth table of the XOR operator.
• XOR Truth Table is the mathematical table constructed using the proper logic of the XOR operator.
• The logic used behind the XOR operator is; whenever XOR operation is applied on the two different bits of two operands, then the result will always produce ‘1’, and if the XOR operation is applied on the two same bits of two operands then the result produces output ‘0’.

Truth Table of Exclusive OR (XOR) operator

Let there are two operands; the First one is A and the second one is B, the total combinations of input formed by these two operands will be 4. By using the following XOR truth table, we will determine the corresponding output. The result will be captured in C, here C = A ^ B.

In this truth table, we are taking input in the form of bits, i.e., 0 and 1, and the output will also be generated in the form of bits, i.e., 0 and 1.

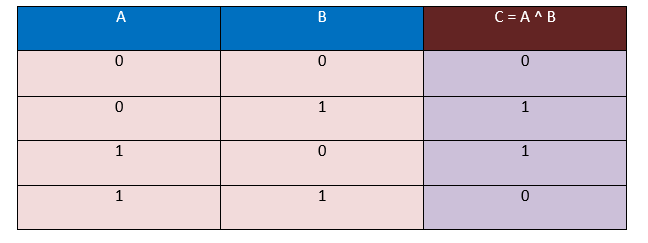
Here, in the above XOR Truth table, we observe that when the values of operands A and B are different, i.e., ( 0, 1 ), ( 1, 0 ), the result that comes out will always be 1. And when the values of operands A and B are the same, i.e., ( 0, 0 ), ( 1, 1 ), the result that comes out will always be 0.

Similarly, in this way, we can draw the truth table for Boolean values –

Let there are two operands; the First one is A and the second one is B. The total combinations of input formed by these two operands will be 4. By using the following XOR truth table, we will determine the corresponding output. The result will be captured in C, here C = A ^ B.

In this truth table, we are taking input in the form of Truth values, i.e., True ( T ) and False ( F ). The output will also be generated in the form of True values, i.e., T and F.

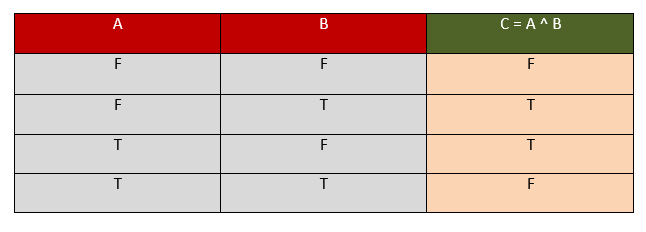
Here, in the above XOR Truth table, we observe that, when the values of operands A and B are different, i.e., ( F, T ), ( T, F ), the result comes out will always be T. And when the values of operands A and B are same, i.e., ( F, F ), ( T, T ), the result comes out will always be F.

From the tables above, we observe that T ( True ) is denoted by one and F ( False ) is denoted by 0.

Steps to solve any given problem –

1. The operands given in the problem will always be in the decimal value.
2. Firstly, we need to convert the values of operands into binary
3. After converting the values of operands in binary numbers, put both operands one over each other.
4. Remember that before applying exclusive OR (XOR) operation on them, kindly check the number of digits in them.
5. If the count of digits does not match, the extra 0’s at the left end of the small operand balances the counts of digits.
6. Finally, with the help of the above truth table, apply the XOR operation on the operands one by one, taking one bit at a time for applying the XOR operation.
7. At last, the result is produced in the form of output.
8. The output is produced will be in binary form, now convert the binary form into decimal form and note down the result value.

Execution of Bitwise Exclusive OR (XOR) operation in C++

Let us understand in more detail about the execution of the XOR operation in C++ with the help of examples –

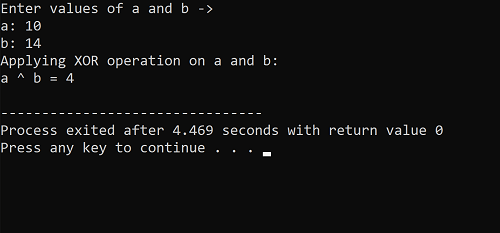
Example 1: Find the exclusive OR of integer values; 10 and 14. Also, explain it and write the code of execution in C++.

Solution: Let us consider two variables,’ a ‘ and ‘ b ‘, to store the corresponding two operands given in the above question, i.e., 10 and 14.

Here, a = 10 and b = 14.

We will follow the below steps to find out the exclusive OR of the given two operands.

1. We know that 10 and 14 are in decimal form, and for applying bitwise XOR operation, it is necessary to convert it into binary form.
2. Binary form ‘ a ‘, i.e., 10 is ‘ 1010 ‘ and Binary form of ‘ b ‘, i.e., 14 is ‘ 1110 ‘.
3. Here we observe that the count of binary digits present in a is four and the count of binary digits present in b is also 4; hence the number of binary digits present in both the variables are the same and already balanced, we do not need to add more number of 0’s to balance it.
4. Now, putting the binary digits present in ‘b’ down to the binary digits present in ‘a’.
5. Finally, applying the XOR operation one by one on the corresponding bits matches and note down the output.
6. The output generated at last will be in binary form, as the above question given in the decimal form, so we need to convert the result in decimal form.

Explanation:

a = 10 ( In Decimal form )

b = 14 ( In Decimal form )

Now, for an XOR b, we need to convert a and b in binary form –

a = 1010 ( In Binary form )

b = 1110 ( In Binary form )

Now, applying XOR operation on a and b –

a = 1010

b = 1110

—————

a ^ b = 0100 ( In Binary form )

The result of a ^ b is 0100, which is in binary form.

Now converting the result in decimal form, which is 4.

10 ^ 14 = 4

NOTE: By using the above XOR truth table, the output of corresponding bits are generated.

We will now apply the bitwise XOR operation on 10 and 14 in C++ language and get the result, i.e., 4.

C++ code for above example:

Output

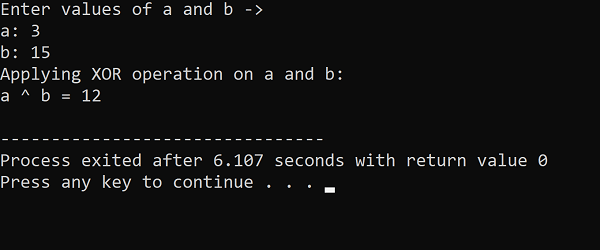
Example 2: Find the exclusive OR of integer values; 3 and 15. Also, explain it and write the code of execution in C++.

Solution: Let us consider two variables,’ a ‘ and ‘ b ‘, to store the corresponding two operands given in the above question, i.e., 3 and 15.

Here, a = 3 and b = 15.

We will follow the below steps to find out the exclusive OR of the given two operands.

1. We know that 3 and 15 are in decimal form, and for applying bitwise XOR operation, it is necessary to convert it into binary form.
2. Binary form ‘ a ‘, i.e., 3 is ’11’ and Binary form of ‘ b ‘, i.e., 15 is ‘1111’.
3. Here we will observe that the count of binary digits present in a is two and the count of binary digits present in b is four; hence the number of binary digits present in both the variables are not the same. Thus, unbalanced, we do need to add more number of 0’s on the left side of the lower binary number, i.e., a, which is ‘11′, to balance it.
4. After balancing, the value of a is ‘ 0011 ‘, and b is ‘ 1111 ‘.
5. Now, putting the binary digits present in ‘ b ‘ down to the binary digits present in ‘ a ‘.
6. Finally, applying the XOR operation one by one on the corresponding bits matches and note down the output.
7. The output generated at last will be in binary form, as the above question given in the decimal form, so we need to convert the result in decimal form.

Explanation:

a = 3 ( In Decimal form )

b = 15 ( In Decimal form )

Now, for an XOR b, we need to convert a and b in binary form –

a = 0011 ( In Binary form )

b = 1111 ( In Binary form )

Now, applying XOR operation on a and b –

a = 0011

b = 1111

—————

a ^ b = 1100 ( In Binary form )

The result of a ^ b is 1100, which is in binary form.

Now converting the result in decimal form, which is 12.

3 ^ 15 = 12

NOTE: By using the above XOR truth table, the output of corresponding bits are generated.

We will now apply the bitwise XOR operation on 3 and 15 in C++ language and get the result, i.e., 12.

C++ code for above example:

Output

---