Linear Regression
Linear regression is used to predict the value of an outcome variable y on the basis of one or more input predictor variables x. In other words, linear regression is used to establish a linear relationship between the predictor and response variables.
In linear regression, predictor and response variables are related through an equation in which the exponent of both these variables is 1. Mathematically, a linear relationship denotes a straight line, when plotted as a graph.
There is the following general mathematical equation for linear regression:
Here,
- y is a response variable.
- x is a predictor variable.
- a and b are constants that are called the coefficients.
Steps for establishing the Regression
The prediction of the weight of a person when his height is known, is a simple example of regression. To predict the weight, we need to have a relationship between the height and weight of a person.
There are the following steps to create the relationship:
- In the first step, we carry out the experiment of gathering a sample of observed values of height and weight.
- After that, we create a relationship model using the lm() function of R.
- Next, we will find the coefficient with the help of the model and create the mathematical equation using this coefficient.
- We will get the summary of the relationship model to understand the average error in prediction, known as residuals.
- At last, we use the predict() function to predict the weight of the new person.
There is the following syntax of lm() function:
Here,
| S.No | Parameters | Description |
|---|---|---|
| 1. | Formula | It is a symbol that presents the relationship between x and y. |
| 2. | Data | It is a vector on which we will apply the formula. |
Creating Relationship Model and Getting the Coefficients
Let’s start performing the second and third steps, i.e., creating a relationship model and getting the coefficients. We will use the lm() function and pass the x and y input vectors and store the result in a variable named relationship_model.
Example
Output:
Call: lm(formula = y ~ x) Coefficients: (Intercept) x 47.50833 0.07276
Getting Summary of Relationship Model
We will use the summary() function to get a summary of the relationship model. Let’s see an example to understand the use of the summary() function.
Example
Output:
Call: lm(formula = y ~ x) Residuals: Min 1Q Median 3Q Max -38.948 -7.390 1.869 15.933 34.087 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 47.50833 55.18118 0.861 0.414 x 0.07276 0.39342 0.185 0.858 Residual standard error: 25.96 on 8 degrees of freedom Multiple R-squared: 0.004257,Adjusted R-squared: -0.1202 F-statistic: 0.0342 on 1 and 8 DF, p-value: 0.8579
The predict() Function
Now, we will predict the weight of new persons with the help of the predict() function. There is the following syntax of predict function:
Here,
| S.No | Parameter | Description |
|---|---|---|
| 1. | object | It is the formula that we have already created using the lm() function. |
| 2. | Newdata | It is the vector that contains the new value for the predictor variable. |
Example
Output:
1 59.14977
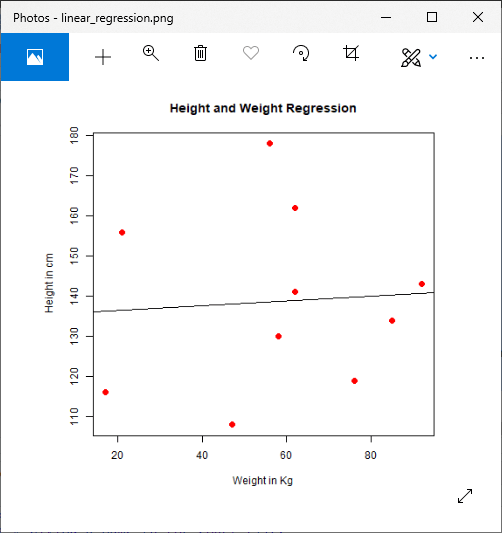
Plotting Regression
Now, we plot out prediction results with the help of the plot() function. This function takes parameter x and y as an input vector and many more arguments.
Example
Output: